| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 5 Prime Time
Welcome to the solution guide for Chapter 5, "Prime Time," a pivotal chapter within the Class 6 Ganita Prakash textbook prescribed by NCERT for the 2024-25 academic session. This chapter significantly deepens the exploration of numbers, focusing specifically on the fascinating and fundamental category of prime numbers and their counterparts, composite numbers. Building upon potentially introductory concepts from earlier studies (like Chapter 3, "Number Play"), these solutions are meticulously crafted to enhance students' understanding, providing clarity and detailed methods for the exercises presented.
The core objective here is to move beyond basic identification and delve into the unique properties that distinguish prime numbers (numbers greater than 1 with exactly two distinct positive divisors: 1 and themselves, like $2, 3, 5, 7, 11, \dots$) from composite numbers (numbers greater than 1 that have more than two factors, like $4, 6, 8, 9, 10, \dots$). The solutions provided offer comprehensive support for exercises designed to solidify this distinction. Students can expect detailed explanations and worked examples focused on systematically identifying prime numbers within a given range. This often involves demonstrating practical techniques such as the Sieve of Eratosthenes, an ancient and effective algorithm for filtering out composite numbers to reveal the primes up to a specific limit.
Beyond the basic definitions, "Prime Time" often introduces related intriguing concepts. The solutions will likely provide clear definitions and illustrative examples for:
- Twin Primes: Pairs of prime numbers that have a difference of exactly 2. Examples include $(3, 5)$, $(5, 7)$, $(11, 13)$, and $(17, 19)$.
- Co-primes (or Relatively Prime numbers): Pairs of numbers whose highest common factor (HCF) is only 1. They don't need to be prime themselves, for instance, $8$ and $15$ are co-prime.
- Perfect Numbers: Although less common at this level, sometimes introduced; these are numbers that are equal to the sum of their proper positive divisors (e.g., $6 = 1 + 2 + 3$).
A central pillar, revisited and reinforced in this chapter, is the concept of prime factorization. This fundamental idea states that every composite number can be expressed as a unique product of its prime factors. The solutions will demonstrate this process clearly, possibly applying it to larger numbers than previously encountered, breaking them down into their prime building blocks (e.g., $84 = 2 \times 2 \times 3 \times 7 = 2^2 \times 3 \times 7$). The uniqueness of this factorization, informally known as the Fundamental Theorem of Arithmetic, is implicitly underscored. Furthermore, the solutions will expertly guide students through various problem types, such as devising tests to determine if a given number is prime, applying the properties of primes to solve numerical puzzles, or investigating interesting patterns related to the distribution or behavior of prime numbers. By carefully studying these detailed solutions for Chapter 5 of the Class 6 Ganita Prakash (2024-25), students will gain a more profound appreciation for the foundational role prime numbers play across mathematics, refine their factorization skills, learn systematic identification methods, and strengthen their overall number sense and analytical thinking capabilities.
Figure it Out (Page 108)

Question 1. At what number is ‘idli-vada’ said for the 10th time?
Answer:
The activity described involves counting numbers from 1 upwards, saying "idli" for multiples of 3, "vada" for multiples of 5, and "idli-vada" for multiples of both 3 and 5 (i.e., multiples of 15).
The phrase "idli-vada" is said for numbers that are multiples of 15.
We are looking for the 10th number at which "idli-vada" is said. This means we are looking for the 10th multiple of 15.
The multiples of 15 are:
$1 \times 15 = 15$ (1st time "idli-vada" is said)
$2 \times 15 = 30$ (2nd time "idli-vada" is said)
$3 \times 15 = 45$ (3rd time "idli-vada" is said)
$4 \times 15 = 60$ (4th time "idli-vada" is said)
$5 \times 15 = 75$ (5th time "idli-vada" is said)
$6 \times 15 = 90$ (6th time "idli-vada" is said)
$7 \times 15 = 105$ (7th time "idli-vada" is said)
$8 \times 15 = 120$ (8th time "idli-vada" is said)
$9 \times 15 = 135$ (9th time "idli-vada" is said)
$10 \times 15 = 150$ (10th time "idli-vada" is said)
The 10th multiple of 15 is $10 \times 15 = 150$.
So, "idli-vada" is said for the 10th time at the number 150.
Question 2. If the game is played for the numbers from 1 till 90, find out:
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
c. How many times would the children say ‘idli-vada’?
Answer:
The game involves saying 'idli' for multiples of 3, 'vada' for multiples of 5, and 'idli-vada' for multiples of both 3 and 5 (which are multiples of 15).
The game is played for numbers from 1 to 90.
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
The word 'idli' is said for all numbers that are multiples of 3, up to 90.
To find the number of multiples of 3 up to 90, we divide 90 by 3.
Number of times 'idli' is said = $\frac{90}{3}$
$= 30$
The children would say ‘idli’ (including 'idli-vada') 30 times.
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
The word 'vada' is said for all numbers that are multiples of 5, up to 90.
To find the number of multiples of 5 up to 90, we divide 90 by 5.
Number of times 'vada' is said = $\frac{90}{5}$
$= 18$
The children would say ‘vada’ (including 'idli-vada') 18 times.
c. How many times would the children say ‘idli-vada’?
The phrase 'idli-vada' is said for all numbers that are multiples of both 3 and 5, i.e., multiples of the least common multiple (LCM) of 3 and 5.
LCM(3, 5) = $3 \times 5 = 15$ (since 3 and 5 are prime numbers).
So, 'idli-vada' is said for multiples of 15, up to 90.
To find the number of multiples of 15 up to 90, we divide 90 by 15.
Number of times 'idli-vada' is said = $\frac{90}{15}$
$= 6$
The children would say ‘idli-vada’ 6 times.
Question 3. What if the game was played till 900? How would your answers change?
Answer:
If the game is played for numbers from 1 to 900, the method to find the number of times 'idli', 'vada', and 'idli-vada' are said remains the same, but we use 900 as the upper limit instead of 90.
a. How many times would the children say ‘idli’ (including the times they say ‘idli-vada’)?
This is the number of multiples of 3 up to 900.
Number of times 'idli' is said = $\frac{900}{3}$
$= 300$
If the game was played till 900, the children would say ‘idli’ (including 'idli-vada') 300 times.
b. How many times would the children say ‘vada’ (including the times they say ‘idli-vada’)?
This is the number of multiples of 5 up to 900.
Number of times 'vada' is said = $\frac{900}{5}$
$= 180$
If the game was played till 900, the children would say ‘vada’ (including 'idli-vada') 180 times.
c. How many times would the children say ‘idli-vada’?
This is the number of multiples of 15 (LCM of 3 and 5) up to 900.
Number of times 'idli-vada' is said = $\frac{900}{15}$
$= 60$
If the game was played till 900, the children would say ‘idli-vada’ 60 times.
Compared to playing till 90:
- The number of times 'idli' is said increases from 30 to 300 (10 times more).
- The number of times 'vada' is said increases from 18 to 180 (10 times more).
- The number of times 'idli-vada' is said increases from 6 to 60 (10 times more).
The answers increase proportionally because 900 is 10 times 90.
Question 4.
Is this figure somehow related to the ‘idli-vada’ game?
Hint: Imagine playing the game till 30. Draw the figure if the game is played till 60.
Answer:
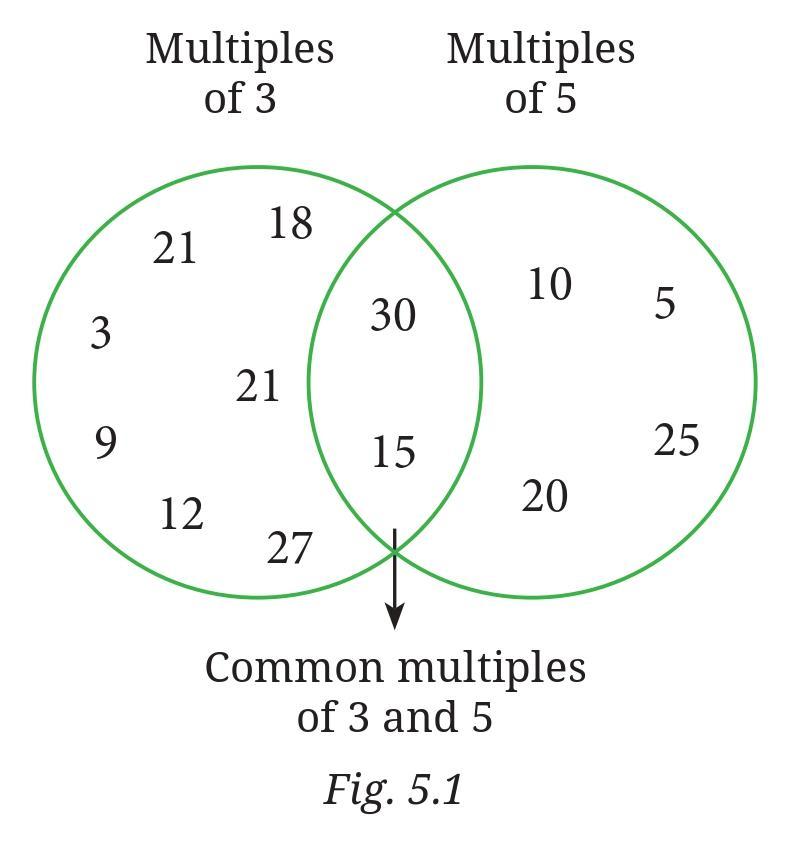
The figure referenced (presumably from Page 108, showing circles with labels) is indeed related to the 'idli-vada' game. The figure likely represents a Venn diagram or similar visual representation of sets.
The game deals with numbers that are multiples of 3, multiples of 5, and multiples of both 3 and 5.
- Numbers where 'idli' is said are multiples of 3.
- Numbers where 'vada' is said are multiples of 5.
- Numbers where 'idli-vada' is said are multiples of both 3 and 5 (multiples of 15).
The figure likely shows two overlapping circles, one representing the set of multiples of 3 and the other representing the set of multiples of 5. The overlapping region represents the numbers that are multiples of both 3 and 5 (multiples of 15).
Playing the game till 30:
- Multiples of 3 up to 30: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 (Total 10)
- Multiples of 5 up to 30: 5, 10, 15, 20, 25, 30 (Total 6)
- Multiples of 15 up to 30: 15, 30 (Total 2)
In a Venn diagram:
- Numbers only in the 'Multiples of 3' circle (saying only 'idli'): 3, 6, 9, 12, 18, 21, 24, 27 (Total 8)
- Numbers only in the 'Multiples of 5' circle (saying only 'vada'): 5, 10, 20, 25 (Total 4)
- Numbers in the overlapping region (saying 'idli-vada'): 15, 30 (Total 2)
Total numbers for which 'idli' is said (only 'idli' + 'idli-vada') = $8 + 2 = 10$. (Matches $30 \div 3$).
Total numbers for which 'vada' is said (only 'vada' + 'idli-vada') = $4 + 2 = 6$. (Matches $30 \div 5$).
Total numbers where *something* is said = $8 + 4 + 2 = 14$.
Numbers where *nothing* is said (neither multiple of 3 nor 5) = Total numbers - Numbers where something is said = $30 - 14 = 16$.
Playing the game till 60:
- Multiples of 3 up to 60: $60 \div 3 = 20$
- Multiples of 5 up to 60: $60 \div 5 = 12$
- Multiples of 15 up to 60: $60 \div 15 = 4$
In a Venn diagram for numbers 1 to 60:
- Multiples of 3 (Total 20)
- Multiples of 5 (Total 12)
- Multiples of 15 (Overlap) (Total 4)
Numbers only 'idli' (Multiples of 3 but not 5) = (Multiples of 3) - (Multiples of 15) = $20 - 4 = 16$.
Numbers only 'vada' (Multiples of 5 but not 3) = (Multiples of 5) - (Multiples of 15) = $12 - 4 = 8$.
Numbers 'idli-vada' (Multiples of 15) = 4.
Total numbers where *something* is said = $16 + 8 + 4 = 28$.
Numbers where *nothing* is said = $60 - 28 = 32$.
The figure is related to the game as it visually represents the sets of numbers for which 'idli', 'vada', or 'idli-vada' are said, showing the overlap where both conditions are met.
Intext Question (Page 108)
Question: Let us now play the ‘idli-vada’ game with different pairs of numbers:
a. 2 and 5,
b. 3 and 7,
c. 4 and 6.
We will say ‘idli’ for multiples of the smaller number, ‘vada’ for multiples of the larger number and ‘idli-vada’ for common multiples. Draw a figure similar to Fig. 5.1 if the game is played up to 60.
Answer:
The game involves saying 'idli' for multiples of the smaller number, 'vada' for multiples of the larger number, and 'idli-vada' for common multiples (multiples of the Least Common Multiple or LCM) up to the number 60.
We will analyze each pair and describe the sets involved, as would be represented in a figure similar to a Venn diagram.
a. Pair: 2 and 5
- Smaller number: 2 (say 'idli' for multiples of 2)
- Larger number: 5 (say 'vada' for multiples of 5)
- Common Multiples: Multiples of LCM(2, 5) = 10 (say 'idli-vada' for multiples of 10)
Playing the game up to 60:
- Numbers where 'idli' is said (multiples of 2 up to 60): $\lfloor 60/2 \rfloor = 30$ numbers.
- Numbers where 'vada' is said (multiples of 5 up to 60): $\lfloor 60/5 \rfloor = 12$ numbers.
- Numbers where 'idli-vada' is said (multiples of 10 up to 60): $\lfloor 60/10 \rfloor = 6$ numbers.
In a figure similar to Fig. 5.1 (a Venn diagram):
- One circle represents "Multiples of 2 (Idli)". It contains 30 numbers in total.
- The other circle represents "Multiples of 5 (Vada)". It contains 12 numbers in total.
- The overlapping region represents "Multiples of 10 (Idli-Vada)". It contains 6 numbers.
- The region only in the 'Multiples of 2' circle (saying only 'idli'): These are multiples of 2 that are not multiples of 10. Count = (Multiples of 2) - (Multiples of 10) = $30 - 6 = 24$ numbers.
- The region only in the 'Multiples of 5' circle (saying only 'vada'): These are multiples of 5 that are not multiples of 10. Count = (Multiples of 5) - (Multiples of 10) = $12 - 6 = 6$ numbers.
- The region outside both circles (saying nothing): These are numbers up to 60 that are neither multiples of 2 nor 5. Count = Total numbers - (Multiples of 2 + Multiples of 5 - Multiples of 10) = $60 - (30 + 12 - 6) = 60 - 36 = 24$ numbers.
The figure would show two overlapping circles labelled "Multiples of 2" and "Multiples of 5". The overlap would be labelled "Multiples of 10". The counts in the respective regions would be 24 (only Idli), 6 (Idli-Vada), and 6 (only Vada). The number 24 would be outside the circles.
b. Pair: 3 and 7
- Smaller number: 3 (say 'idli' for multiples of 3)
- Larger number: 7 (say 'vada' for multiples of 7)
- Common Multiples: Multiples of LCM(3, 7). Since 3 and 7 are prime, LCM(3, 7) = $3 \times 7 = 21$. (say 'idli-vada' for multiples of 21)
Playing the game up to 60:
- Numbers where 'idli' is said (multiples of 3 up to 60): $\lfloor 60/3 \rfloor = 20$ numbers.
- Numbers where 'vada' is said (multiples of 7 up to 60): $\lfloor 60/7 \rfloor = 8$ numbers.
- Numbers where 'idli-vada' is said (multiples of 21 up to 60): $\lfloor 60/21 \rfloor = 2$ numbers (21, 42).
In a figure similar to Fig. 5.1 (a Venn diagram):
- One circle represents "Multiples of 3 (Idli)". It contains 20 numbers in total.
- The other circle represents "Multiples of 7 (Vada)". It contains 8 numbers in total.
- The overlapping region represents "Multiples of 21 (Idli-Vada)". It contains 2 numbers.
- The region only in the 'Multiples of 3' circle (saying only 'idli'): $20 - 2 = 18$ numbers.
- The region only in the 'Multiples of 7' circle (saying only 'vada'): $8 - 2 = 6$ numbers.
- The region outside both circles (saying nothing): $60 - (20 + 8 - 2) = 60 - 26 = 34$ numbers.
The figure would show two overlapping circles labelled "Multiples of 3" and "Multiples of 7". The overlap would be labelled "Multiples of 21". The counts in the respective regions would be 18 (only Idli), 2 (Idli-Vada), and 6 (only Vada). The number 34 would be outside the circles.
c. Pair: 4 and 6
- Smaller number: 4 (say 'idli' for multiples of 4)
- Larger number: 6 (say 'vada' for multiples of 6)
- Common Multiples: Multiples of LCM(4, 6). LCM(4, 6) = 12. (say 'idli-vada' for multiples of 12)
Playing the game up to 60:
- Numbers where 'idli' is said (multiples of 4 up to 60): $\lfloor 60/4 \rfloor = 15$ numbers.
- Numbers where 'vada' is said (multiples of 6 up to 60): $\lfloor 60/6 \rfloor = 10$ numbers.
- Numbers where 'idli-vada' is said (multiples of 12 up to 60): $\lfloor 60/12 \rfloor = 5$ numbers.
In a figure similar to Fig. 5.1 (a Venn diagram):
- One circle represents "Multiples of 4 (Idli)". It contains 15 numbers in total.
- The other circle represents "Multiples of 6 (Vada)". It contains 10 numbers in total.
- The overlapping region represents "Multiples of 12 (Idli-Vada)". It contains 5 numbers.
- The region only in the 'Multiples of 4' circle (saying only 'idli'): $15 - 5 = 10$ numbers.
- The region only in the 'Multiples of 6' circle (saying only 'vada'): $10 - 5 = 5$ numbers.
- The region outside both circles (saying nothing): $60 - (15 + 10 - 5) = 60 - 20 = 40$ numbers.
The figure would show two overlapping circles labelled "Multiples of 4" and "Multiples of 6". The overlap would be labelled "Multiples of 12". The counts in the respective regions would be 10 (only Idli), 5 (Idli-Vada), and 5 (only Vada). The number 40 would be outside the circles.
Intext Question (Page 109)
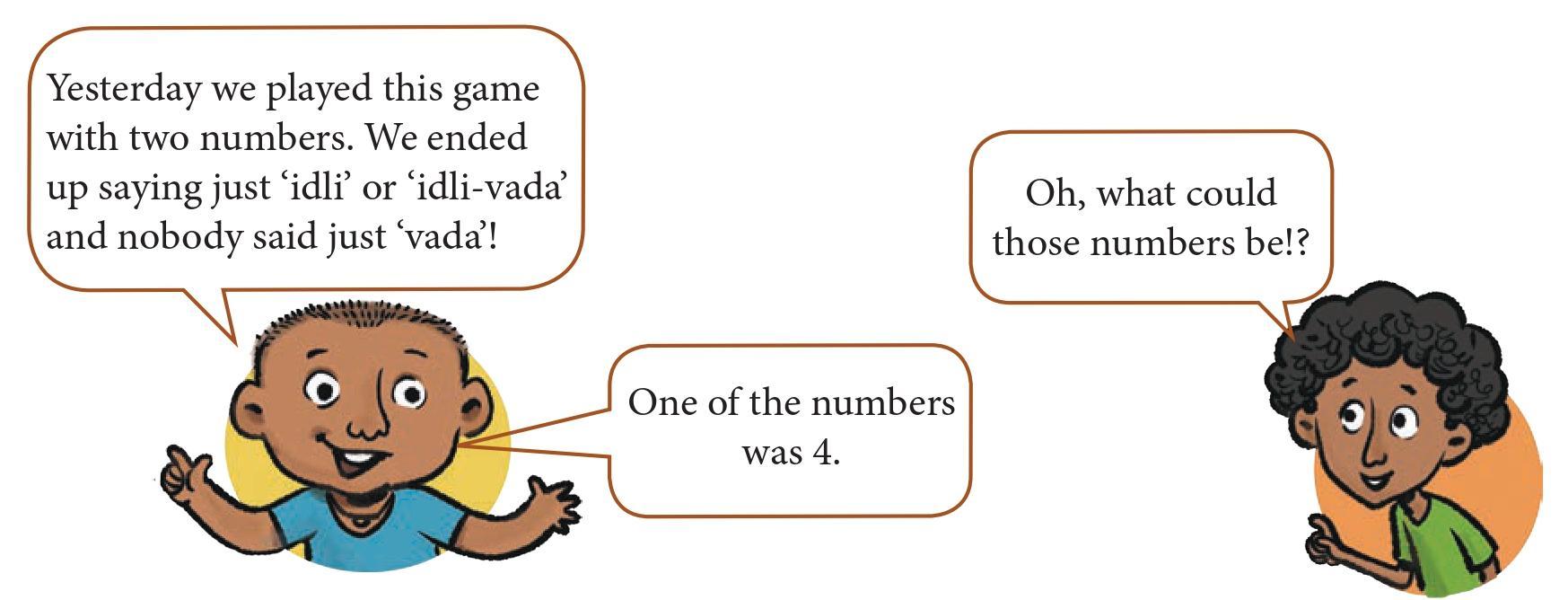
Question: Which of the following could be the other number:
2, 3, 5, 8, 10?
Answer:
This question refers to the context on Page 108, specifically the example involving the numbers 4 and another number in the 'idli-vada' game, where 'idli' is for multiples of 4 and 'vada' is for multiples of the other number.
The image on Page 108 shows a Venn diagram related to the numbers 4 and 6, indicating that common multiples are multiples of 12. In that specific example, the pair of numbers was 4 and 6.
The question asks which of the given numbers (2, 3, 5, 8, 10) could be the "other number" when the first number is 4.
The game rule is: 'idli' for multiples of the smaller number, 'vada' for multiples of the larger number, and 'idli-vada' for common multiples (multiples of the LCM).
Let the other number be $x$. The pair of numbers is 4 and $x$.
The common multiples are multiples of LCM($4, x$).
We need to check which value of $x$ from the list {2, 3, 5, 8, 10} would make sense in a context where the common multiples are shown (likely referring back to the original idli-vada game implicitly or explicitly where common multiples played a role).
Let's calculate the LCM of 4 and each number in the list:
- If $x=2$: LCM(4, 2) = 4. Multiples of 4 are 4, 8, 12, ... (These are also multiples of 2). Common multiples are multiples of 4.
- If $x=3$: LCM(4, 3) = 12. Common multiples are multiples of 12.
- If $x=5$: LCM(4, 5) = 20. Common multiples are multiples of 20.
- If $x=8$: LCM(4, 8) = 8. Multiples of 8 are 8, 16, 24, ... (These are also multiples of 4). Common multiples are multiples of 8.
- If $x=10$: LCM(4, 10) = 20. Common multiples are multiples of 20.
The intext question on Page 108 is likely directly related to the example on that page, which uses the pair 4 and 6, with common multiples being multiples of 12. The previous "idli-vada" game used 3 and 5, with common multiples being multiples of 15.
The options provided are {2, 3, 5, 8, 10}. If the first number is 4, which of these could be the "other number" to produce a scenario related to the game?
Let's re-examine the figure on Page 108. It explicitly shows a Venn diagram with one circle for multiples of 4, another for multiples of 6, and the overlap for multiples of 12. This figure is presented immediately before the intext question.
The question "Which of the following could be the other number" refers to the pair of numbers being considered in the context, where one number is 4. Based on the preceding figure and discussion on page 108, the pair of numbers being implicitly referred to is (4 and 6).
The question asks which of the numbers in the list {2, 3, 5, 8, 10} could be the "other number" in a similar scenario involving 4. The number 6 is not in the list.
Let's re-read the context carefully. The section "Playing with Multiples" leads into the idli-vada game with 3 and 5 (multiples of 15). Then it shows a figure related to 4 and 6 (multiples of 12). The intext question follows this.
The question asks "Which of the following could be the other number:" and lists 2, 3, 5, 8, 10. This suggests one of these numbers, when paired with 4, fits a pattern or scenario relevant to the game or the preceding discussion.
The most likely interpretation is that the question is asking which of the listed numbers, when paired with 4, results in a situation where the LCM is a value that appeared in the previous examples (LCM=15 for 3 & 5, or LCM=12 for 4 & 6). Let's check the LCMs again:
- LCM(4, 2) = 4
- LCM(4, 3) = 12
- LCM(4, 5) = 20
- LCM(4, 8) = 8
- LCM(4, 10) = 20
Among the listed options, pairing 4 with 3 gives an LCM of 12, which is the LCM used in the figure involving 4 and 6. This suggests that the question might be related to finding a pair (4, x) from the list such that LCM(4, x) = LCM(4, 6) = 12.
Let's consider the pairs (4, 2), (4, 3), (4, 5), (4, 8), (4, 10).
The figure shown is a Venn diagram for multiples of 4 and multiples of 6, with overlap as multiples of 12.
If the other number were 2, the common multiples of 4 and 2 are multiples of 4 (since 4 is a multiple of 2). LCM(4, 2) = 4.
If the other number were 3, the common multiples of 4 and 3 are multiples of 12. LCM(4, 3) = 12.
If the other number were 5, the common multiples of 4 and 5 are multiples of 20. LCM(4, 5) = 20.
If the other number were 8, the common multiples of 4 and 8 are multiples of 8. LCM(4, 8) = 8.
If the other number were 10, the common multiples of 4 and 10 are multiples of 20. LCM(4, 10) = 20.
The question immediately follows the figure related to 4 and 6, where the common multiples are multiples of 12. Among the options, pairing 4 with 3 results in common multiples being multiples of 12 (LCM(4, 3) = 12).
It seems the question is designed to make the student connect the LCM from the previous example (LCM of 4 and 6 is 12) with the list of options to find a number ($x$) such that LCM($4, x$) results in a previously encountered LCM (either 12 or 15). Only $x=3$ gives LCM(4, 3) = 12.
Therefore, the other number could be 3, as the pair (4, 3) results in common multiples being multiples of 12, which is the LCM for the pair (4, 6) shown in the figure.
The other number could be 3.
Intext Question (Page 110)
Jump Jackpot
Jumpy and Grumpy play a game.
- Grumpy places a treasure on some number. For example, he may place it on 24.
- Jumpy chooses a jump size. If he chooses 4, then he has to jump only on multiples of 4, starting at 0.
- Jumpy gets the treasure if he lands on the number where Grumpy placed it.
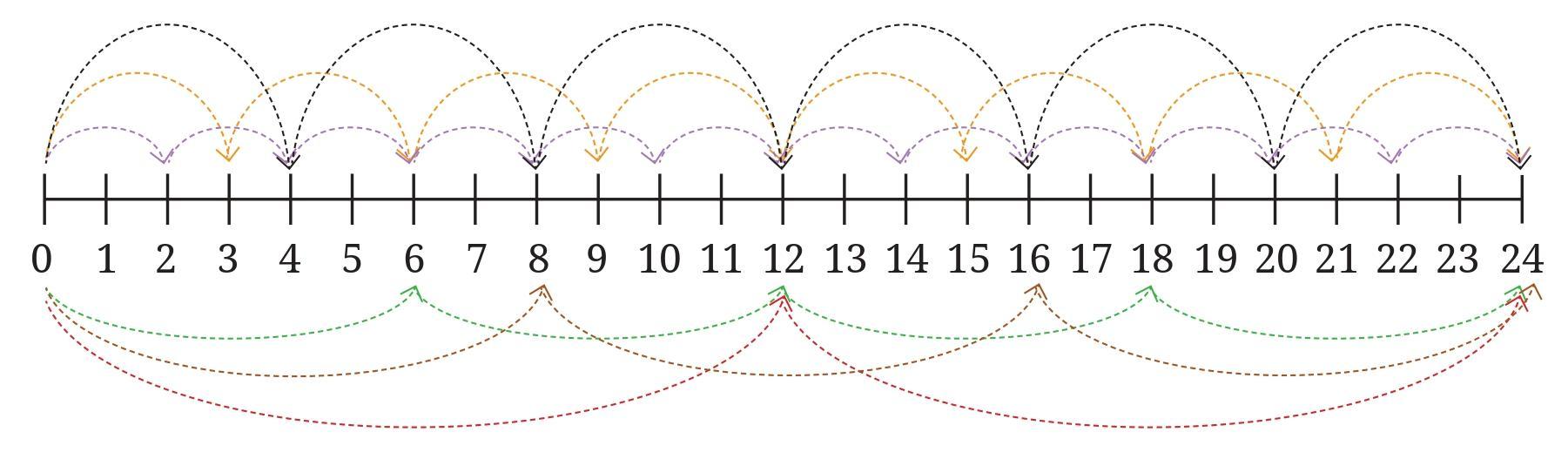
Question: What jump size can reach both 15 and 30? There are multiple jump sizes possible. Try to find them all.
Answer:
In the Jump Jackpot game, Jumpy starts at 0 and makes jumps of a fixed size. To reach a specific number, that number must be a multiple of the chosen jump size.
We want to find the jump sizes that can reach both 15 and 30.
This means that both 15 and 30 must be multiples of the jump size.
In other words, the jump size must be a common divisor of 15 and 30.
First, let's find the divisors of 15.
The divisors of 15 are the numbers that divide 15 evenly:
1, 3, 5, 15.
Next, let's find the divisors of 30.
The divisors of 30 are the numbers that divide 30 evenly:
1, 2, 3, 5, 6, 10, 15, 30.
Now, we find the common divisors by looking for the numbers that appear in both lists of divisors.
Common divisors of 15 and 30 are:
1, 3, 5, 15.
These common divisors are the possible jump sizes that Jumpy can choose to land on both 15 and 30.
For example:
- If the jump size is 1, Jumpy lands on 1, 2, 3, ..., 15, ..., 30, ... (reaches both)
- If the jump size is 3, Jumpy lands on 3, 6, 9, 12, 15, 18, ..., 30, ... (reaches both)
- If the jump size is 5, Jumpy lands on 5, 10, 15, 20, 25, 30, ... (reaches both)
- If the jump size is 15, Jumpy lands on 15, 30, 45, ... (reaches both)
The possible jump sizes that can reach both 15 and 30 are 1, 3, 5, and 15.
Intext Question (Page 110)
Question: Look at the table below. What do you notice?
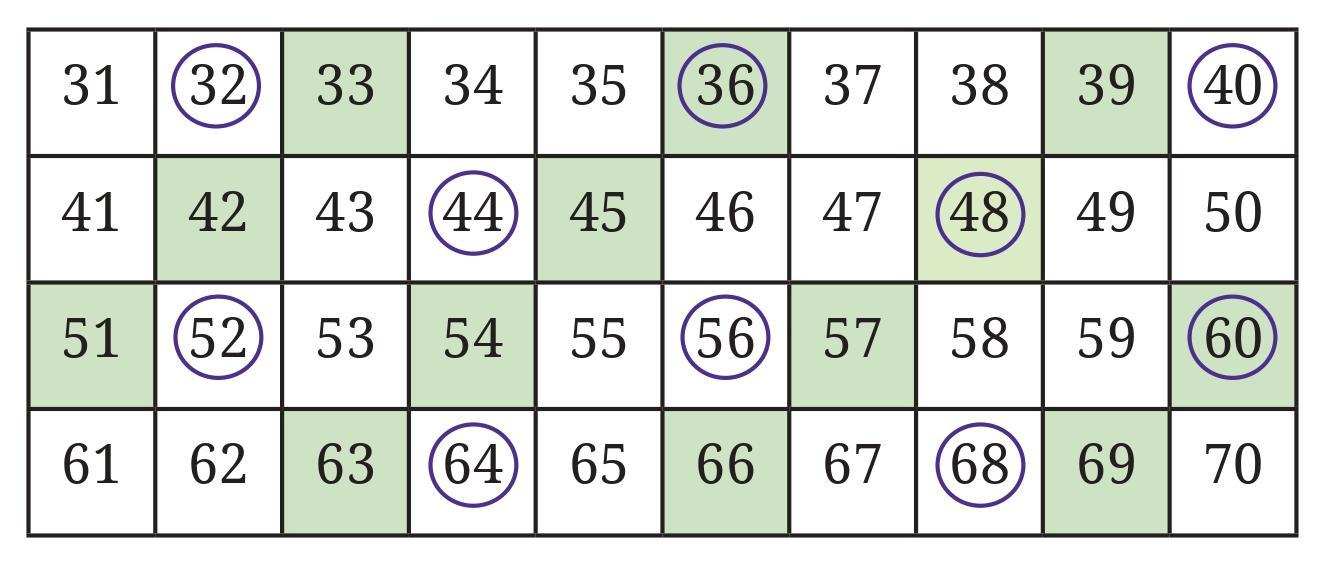
In the table,
1. Is there anything common among the shaded numbers?
2. Is there anything common among the circled numbers?
3. Which numbers are both shaded and circled? What are these numbers called?
Answer:
The table shows numbers from 1 to 60. Some numbers are shaded, some are circled, and some are both.
Let's list the shaded numbers and circled numbers based on the image:
Shaded numbers: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60
Circled numbers: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60
What do you notice?
I notice that the shaded numbers are multiples of 3.
I notice that the circled numbers are multiples of 5.
I notice that some numbers are both shaded and circled.
1. Is there anything common among the shaded numbers?
Yes, all the shaded numbers are multiples of 3.
2. Is there anything common among the circled numbers?
Yes, all the circled numbers are multiples of 5.
3. Which numbers are both shaded and circled? What are these numbers called?
The numbers that are both shaded and circled are the numbers that are present in both the list of shaded numbers and the list of circled numbers.
These numbers are: 15, 30, 45, 60.
These numbers are multiples of both 3 and 5. Numbers that are multiples of both 3 and 5 are multiples of their least common multiple, which is LCM(3, 5) = 15. These numbers (15, 30, 45, 60) are indeed multiples of 15.
These numbers are called common multiples of 3 and 5.
Figure it Out (Page 110 - 111)
Question 1. Find all multiples of 40 that lie between 310 and 410.
Answer:
We need to find the numbers that are multiples of 40 and are greater than 310 but less than 410.
Let the multiples of 40 be represented as $40 \times k$, where $k$ is an integer.
We are looking for values of $40 \times k$ such that:
$310 < 40 \times k < 410$
To find the possible integer values of $k$, we can divide the inequality by 40:
$\frac{310}{40} < k < \frac{410}{40}$
Simplify the fractions:
$\frac{31}{4} < k < \frac{41}{4}$
Convert the fractions to decimals:
$7.75 < k < 10.25$
We are looking for integer values of $k$ that are greater than 7.75 and less than 10.25.
The integers that satisfy this condition are 8, 9, and 10.
Now, we find the multiples of 40 corresponding to these values of $k$:
- For $k=8$: $40 \times 8 = 320$
- For $k=9$: $40 \times 9 = 360$
- For $k=10$: $40 \times 10 = 400$
Let's check if these multiples lie between 310 and 410:
- Is $310 < 320 < 410$? Yes.
- Is $310 < 360 < 410$? Yes.
- Is $310 < 400 < 410$? Yes.
These are the only integer values of $k$ that satisfy the condition, so these are all the multiples of 40 between 310 and 410.
The multiples of 40 that lie between 310 and 410 are 320, 360, and 400.
Question 2. Who am I?
a. I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
b. I am a number less than 100. Two of my factors are 3 and 5. One of my digits is 1 more than the other.
Answer:
Let's solve each riddle:
a. I am a number less than 40. One of my factors is 7. The sum of my digits is 8.
The number must be a multiple of 7 and less than 40.
Let's list the multiples of 7:
$7, 14, 21, 28, 35, 42, \dots$
We only consider multiples less than 40: $7, 14, 21, 28, 35$.
Now, let's check the sum of the digits for each of these numbers:
- For 7: Sum of digits = 7. (Not 8)
- For 14: Sum of digits = $1 + 4 = 5$. (Not 8)
- For 21: Sum of digits = $2 + 1 = 3$. (Not 8)
- For 28: Sum of digits = $2 + 8 = 10$. (Not 8)
- For 35: Sum of digits = $3 + 5 = 8$. (This matches!)
The number that satisfies all conditions is 35.
So, the number is 35.
b. I am a number less than 100. Two of my factors are 3 and 5. One of my digits is 1 more than the other.
Since the number has factors 3 and 5, it must be a common multiple of 3 and 5. The smallest common multiple is the Least Common Multiple (LCM) of 3 and 5. Since 3 and 5 are prime numbers, LCM(3, 5) = $3 \times 5 = 15$.
So, the number must be a multiple of 15 and less than 100.
Let's list the multiples of 15 less than 100:
$15 \times 1 = 15$
$15 \times 2 = 30$
$15 \times 3 = 45$
$15 \times 4 = 60$
$15 \times 5 = 75$
$15 \times 6 = 90$
$15 \times 7 = 105$ (Greater than 100, stop)
The possible numbers are: $15, 30, 45, 60, 75, 90$.
Now, let's check the digits of each of these numbers to see if one digit is 1 more than the other:
- For 15: Digits are 1 and 5. Difference is $5 - 1 = 4$. (Not 1)
- For 30: Digits are 3 and 0. Difference is $3 - 0 = 3$. (Not 1)
- For 45: Digits are 4 and 5. Difference is $5 - 4 = 1$. (This matches!)
- For 60: Digits are 6 and 0. Difference is $6 - 0 = 6$. (Not 1)
- For 75: Digits are 7 and 5. Difference is $7 - 5 = 2$. (Not 1)
- For 90: Digits are 9 and 0. Difference is $9 - 0 = 9$. (Not 1)
The number that satisfies all conditions is 45.
So, the number is 45.
Question 3. A number for which the sum of all its factors is equal to twice the number is called a perfect number. The number 28 is a perfect number. Its factors are 1, 2, 4, 7, 14 and 28. Their sum is 56 which is twice 28. Find a perfect number between 1 and 10.
Answer:
A perfect number is a number where the sum of all its factors is equal to twice the number itself.
We need to find a perfect number that is between 1 and 10. The numbers between 1 and 10 are 2, 3, 4, 5, 6, 7, 8, 9.
Let's find the factors and the sum of factors for each number in this range:
Number 2:
Factors of 2 are 1, 2.
Sum of factors = $1 + 2 = 3$.
Twice the number = $2 \times 2 = 4$.
Sum of factors (3) is not equal to twice the number (4).
Number 3:
Factors of 3 are 1, 3.
Sum of factors = $1 + 3 = 4$.
Twice the number = $2 \times 3 = 6$.
Sum of factors (4) is not equal to twice the number (6).
Number 4:
Factors of 4 are 1, 2, 4.
Sum of factors = $1 + 2 + 4 = 7$.
Twice the number = $2 \times 4 = 8$.
Sum of factors (7) is not equal to twice the number (8).
Number 5:
Factors of 5 are 1, 5.
Sum of factors = $1 + 5 = 6$.
Twice the number = $2 \times 5 = 10$.
Sum of factors (6) is not equal to twice the number (10).
Number 6:
Factors of 6 are 1, 2, 3, 6.
Sum of factors = $1 + 2 + 3 + 6 = 12$.
Twice the number = $2 \times 6 = 12$.
Sum of factors (12) is equal to twice the number (12).
Thus, 6 is a perfect number.
We have found a perfect number (6) between 1 and 10. We can stop here, but let's quickly check the remaining numbers for completeness.
Number 7:
Factors of 7 are 1, 7.
Sum of factors = $1 + 7 = 8$. Twice the number = $2 \times 7 = 14$. $8 \neq 14$.
Number 8:
Factors of 8 are 1, 2, 4, 8.
Sum of factors = $1 + 2 + 4 + 8 = 15$. Twice the number = $2 \times 8 = 16$. $15 \neq 16$.
Number 9:
Factors of 9 are 1, 3, 9.
Sum of factors = $1 + 3 + 9 = 13$. Twice the number = $2 \times 9 = 18$. $13 \neq 18$.
The only perfect number between 1 and 10 is 6.
A perfect number between 1 and 10 is 6.
Question 4. Find the common factors of:
a. 20 and 28
b. 35 and 50
c. 4, 8 and 12
d. 5, 15 and 25
Answer:
To find the common factors of two or more numbers, we first list the factors of each number and then identify the factors that are common to all the lists.
a. Common factors of 20 and 28
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 28: 1, 2, 4, 7, 14, 28
The numbers that appear in both lists are 1, 2, and 4.
The common factors of 20 and 28 are 1, 2, and 4.
b. Common factors of 35 and 50
Factors of 35: 1, 5, 7, 35
Factors of 50: 1, 2, 5, 10, 25, 50
The numbers that appear in both lists are 1 and 5.
The common factors of 35 and 50 are 1 and 5.
c. Common factors of 4, 8 and 12
Factors of 4: 1, 2, 4
Factors of 8: 1, 2, 4, 8
Factors of 12: 1, 2, 3, 4, 6, 12
The numbers that appear in all three lists are 1, 2, and 4.
The common factors of 4, 8 and 12 are 1, 2, and 4.
d. Common factors of 5, 15 and 25
Factors of 5: 1, 5
Factors of 15: 1, 3, 5, 15
Factors of 25: 1, 5, 25
The numbers that appear in all three lists are 1 and 5.
The common factors of 5, 15 and 25 are 1 and 5.
Question 5. Find any three numbers that are multiples of 25 but not multiples of 50.
Answer:
We are looking for numbers that are multiples of 25 but are not multiples of 50.
Let's list the multiples of 25:
Multiples of 25 are $25 \times 1 = 25$, $25 \times 2 = 50$, $25 \times 3 = 75$, $25 \times 4 = 100$, $25 \times 5 = 125$, $25 \times 6 = 150$, and so on.
Multiples of 25: 25, 50, 75, 100, 125, 150, 175, 200, 225, 250, ...
Now, let's list the multiples of 50:
Multiples of 50 are $50 \times 1 = 50$, $50 \times 2 = 100$, $50 \times 3 = 150$, $50 \times 4 = 200$, $50 \times 5 = 250$, and so on.
Multiples of 50: 50, 100, 150, 200, 250, ...
A number is a multiple of 50 if it can be written as $50 \times k$ for some integer $k$. Since $50 = 2 \times 25$, any multiple of 50 can be written as $(2 \times 25) \times k = 25 \times (2k)$. This means that any multiple of 50 is also a multiple of 25.
We are looking for multiples of 25 that are *not* multiples of 50. These are the multiples of 25 that are not even multiples of 25.
Consider the multiples of 25 in the form $25 \times k$:
- If $k$ is an even number ($k = 2m$), then $25 \times k = 25 \times (2m) = 50m$, which is a multiple of 50.
- If $k$ is an odd number ($k = 2m + 1$), then $25 \times k = 25 \times (2m + 1) = 50m + 25$. This number is a multiple of 25, but it is not a multiple of 50 because it leaves a remainder of 25 when divided by 50.
So, the multiples of 25 that are not multiples of 50 are obtained by multiplying 25 by an odd integer.
Let's find the first few multiples of 25 by odd integers (1, 3, 5, 7, ...):
- $25 \times 1 = 25$ (25 is a multiple of 25, but not 50)
- $25 \times 3 = 75$ (75 is a multiple of 25, but not 50)
- $25 \times 5 = 125$ (125 is a multiple of 25, but not 50)
- $25 \times 7 = 175$ (175 is a multiple of 25, but not 50)
- $25 \times 9 = 225$ (225 is a multiple of 25, but not 50)
We need to find any three such numbers.
Three numbers that are multiples of 25 but not multiples of 50 are 25, 75, and 125.
Question 6. Anshu and his friends play the ‘idli-vada’ game with two numbers, which are both smaller than 10. The first time anybody says ‘idlivada’ is after the number 50. What could the two numbers be which are assigned ‘idli’ and ‘vada’?
Answer:
In the 'idli-vada' game, 'idli-vada' is said for numbers that are common multiples of the two assigned numbers.
The two numbers are both smaller than 10.
The first time 'idli-vada' is said is after the number 50. This means the smallest number for which 'idli-vada' is said is greater than 50.
The smallest common multiple of two numbers is their Least Common Multiple (LCM).
So, we are looking for two numbers, say $a$ and $b$, such that:
- $a < 10$ and $b < 10$
- $a$ and $b$ are positive integers.
- The first number that is a multiple of both $a$ and $b$ (i.e., LCM($a, b$)) is greater than 50.
We need to find a pair of distinct integers $(a, b)$ where $1 \le a, b \le 9$, $a \neq b$, such that LCM($a, b$) is just above 50. However, the question says "The first time anybody says ‘idlivada’ is after the number 50". This means the smallest common multiple must be the smallest multiple of LCM($a, b$) that is greater than 50. But the wording likely implies that the LCM itself is just above 50 or is the smallest common multiple they reach that is greater than 50.
Let's interpret "The first time anybody says ‘idlivada’ is after the number 50" as the smallest common multiple (LCM) of the two numbers is a value $M$ such that $M > 50$. But this doesn't seem right because the game is played on numbers sequentially. If the LCM is, say, 55, then 55 is the first number where 'idli-vada' is said. This number 55 is after 50.
Let's reinterpret "The first time anybody says ‘idlivada’ is after the number 50" to mean that all common multiples up to 50 are skipped, and the very next common multiple they encounter is the first one they say "idli-vada" for *in this specific game context*. This sounds like the previous common multiples were somehow excluded. However, the game description suggests they count from 1 upwards.
A simpler interpretation: The smallest common multiple of the two numbers is greater than 50. That is, LCM($a, b$) > 50.
Let's check pairs of numbers less than 10 and calculate their LCMs:
- Pairs involving 9:
- Pairs involving 8 (not already covered):
- Pairs involving 7 (not already covered):
- Pairs involving 6 (not already covered):
- Pairs involving 5 (not already covered):
- Pairs involving 4 (not already covered):
- Pairs involving 3 (not already covered):
LCM(9, 8) = 72 (72 > 50) - Possible pair (9, 8)
LCM(9, 7) = 63 (63 > 50) - Possible pair (9, 7)
LCM(9, 6) = 18 (18 $\not>$ 50)
LCM(9, 5) = 45 (45 $\not>$ 50)
LCM(9, 4) = 36 (36 $\not>$ 50)
LCM(9, 2) = 18 (18 $\not>$ 50)
LCM(8, 7) = 56 (56 > 50) - Possible pair (8, 7)
LCM(8, 6) = 24 (24 $\not>$ 50)
LCM(8, 5) = 40 (40 $\not>$ 50)
LCM(8, 3) = 24 (24 $\not>$ 50)
LCM(8, 2) = 8 (8 $\not>$ 50)
LCM(7, 6) = 42 (42 $\not>$ 50)
LCM(7, 5) = 35 (35 $\not>$ 50)
LCM(7, 4) = 28 (28 $\not>$ 50)
LCM(7, 3) = 21 (21 $\not>$ 50)
LCM(7, 2) = 14 (14 $\not>$ 50)
LCM(6, 5) = 30 (30 $\not>$ 50)
LCM(6, 4) = 12 (12 $\not>$ 50)
LCM(6, 2) = 6 (6 $\not>$ 50)
LCM(5, 4) = 20 (20 $\not>$ 50)
LCM(5, 3) = 15 (15 $\not>$ 50)
LCM(5, 2) = 10 (10 $\not>$ 50)
LCM(4, 3) = 12 (12 $\not>$ 50)
LCM(4, 2) = 4 (4 $\not>$ 50)
LCM(3, 2) = 6 (6 $\not>$ 50)
The pairs of numbers less than 10 whose LCM is greater than 50 are (9, 8), (9, 7), and (8, 7). These pairs result in the first common multiple (LCM) being 72, 63, and 56 respectively, all of which are after 50.
The question asks "What could the two numbers be". Any of these pairs is a valid answer.
Possible pairs for the two numbers are (9 and 8), (9 and 7), or (8 and 7).
For example, if the numbers are 8 and 7, the multiples of 8 are 8, 16, 24, 32, 40, 48, 56, ... and the multiples of 7 are 7, 14, 21, 28, 35, 42, 49, 56, ... The first number common to both lists after 50 is 56 (which is LCM(8, 7)).
Question 7. In the treasure hunting game, Grumpy has kept treasures on 28 and 70. What jump sizes will land on both the numbers?
Answer:
In the treasure hunting game, Jumpy can land on a number if that number is a multiple of the chosen jump size. To land on both 28 and 70, both 28 and 70 must be multiples of the jump size.
This means the jump size must be a common divisor of 28 and 70.
First, let's find the divisors of 28.
The divisors of 28 are the numbers that divide 28 evenly:
1, 2, 4, 7, 14, 28.
Next, let's find the divisors of 70.
The divisors of 70 are the numbers that divide 70 evenly:
1, 2, 5, 7, 10, 14, 35, 70.
Now, we find the common divisors by looking for the numbers that appear in both lists of divisors.
Common divisors of 28 and 70 are:
1, 2, 7, 14.
These common divisors are the possible jump sizes that will land on both 28 and 70.
For example:
- If the jump size is 1, Jumpy lands on 28 and 70.
- If the jump size is 2, Jumpy lands on 28 ($2 \times 14$) and 70 ($2 \times 35$).
- If the jump size is 7, Jumpy lands on 28 ($7 \times 4$) and 70 ($7 \times 10$).
- If the jump size is 14, Jumpy lands on 28 ($14 \times 2$) and 70 ($14 \times 5$).
The jump sizes that will land on both 28 and 70 are 1, 2, 7, and 14.
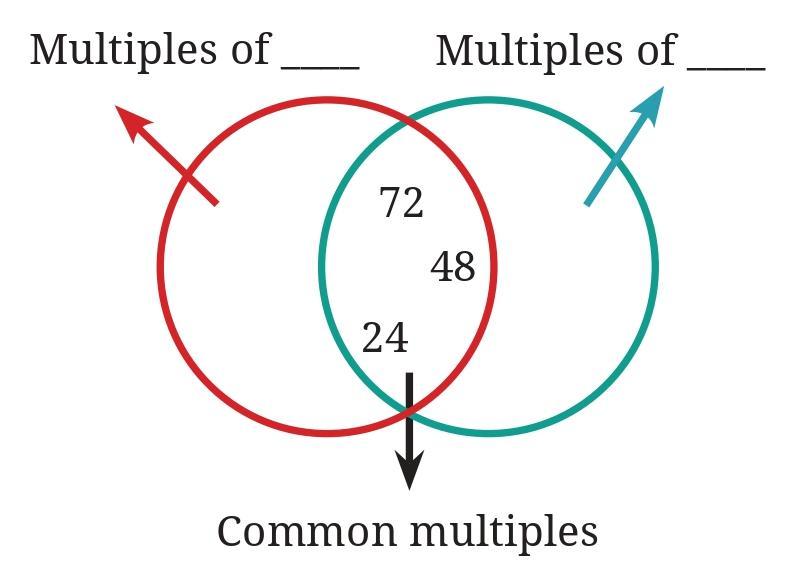
Answer:
The diagram shows a Venn diagram with two overlapping circles labeled "Multiples of $A$" and "Multiples of $B$". The numbers in the overlapping region are the common multiples of $A$ and $B$. The numbers given in the overlapping region are 12, 24, 36, 48, 60.
The numbers in the overlapping region are the common multiples of the two numbers $A$ and $B$. The smallest common multiple is the Least Common Multiple (LCM) of $A$ and $B$.
The common multiples shown are 12, 24, 36, 48, 60. These are all multiples of 12 ($12 \times 1, 12 \times 2, 12 \times 3, 12 \times 4, 12 \times 5$).
This indicates that the Least Common Multiple (LCM) of the two numbers $A$ and $B$ is 12. So, LCM($A, B$) = 12.
We need to find two numbers $A$ and $B$ whose LCM is 12. $A$ and $B$ are likely the numbers whose multiples are being considered in the game, as in the 'idli-vada' examples.
Possible pairs of numbers whose LCM is 12 include:
- LCM(1, 12) = 12
- LCM(2, 12) = 12
- LCM(3, 12) = 12
- LCM(4, 12) = 12
- LCM(6, 12) = 12
- LCM(2, 6) = 6 (Not 12)
- LCM(3, 4) = 12
- LCM(3, 6) = 6 (Not 12)
- LCM(4, 6) = 12
Considering the typical numbers used in such games (smaller integers), common pairs whose LCM is 12 are (3, 4) and (4, 6).
Let's assume the two numbers $A$ and $B$ are 4 and 6, as used in the example on page 108.
If $A=4$ and $B=6$, then LCM(4, 6) = 12. Multiples of 4 are in the left circle, multiples of 6 are in the right circle, and common multiples (multiples of 12) are in the overlap.
Now, let's fill in the missing numbers in the empty regions (assuming the diagram is meant to show numbers up to a certain limit, like 60, as in previous examples).
Left Circle (Multiples of 4, but not Multiples of 6) - numbers that are multiples of 4 but not multiples of 12, up to 60:
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60
Multiples of 12: 12, 24, 36, 48, 60
Multiples of 4 that are not multiples of 12: 4, 8, 16, 20, 28, 32, 40, 44, 52, 56.
These numbers should be in the left-only region of the Venn diagram.
Right Circle (Multiples of 6, but not Multiples of 4) - numbers that are multiples of 6 but not multiples of 12, up to 60:
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
Multiples of 12: 12, 24, 36, 48, 60
Multiples of 6 that are not multiples of 12: 6, 18, 30, 42, 54.
These numbers should be in the right-only region of the Venn diagram.
Assuming the diagram covers numbers up to 60 (as in the previous intext question on page 108), the region outside both circles would contain numbers from 1 to 60 that are neither multiples of 4 nor 6.
Total numbers up to 60 = 60.
Multiples of 4 up to 60 = 15.
Multiples of 6 up to 60 = 10.
Multiples of 12 up to 60 = 5.
Number of multiples of 4 or 6 = (Multiples of 4) + (Multiples of 6) - (Multiples of 12) = $15 + 10 - 5 = 20$.
Numbers outside both circles = Total numbers - (Numbers in the circles) = $60 - 20 = 40$.
The numbers outside would be all numbers from 1 to 60 that are not in the regions described above.
Conclusion:
The two numbers ($A$ and $B$) are likely 4 and 6, as their LCM is 12, and the common multiples shown are multiples of 12.
Filling the Missing Numbers:
- Region only in "Multiples of 4": 4, 8, 16, 20, 28, 32, 40, 44, 52, 56
- Region only in "Multiples of 6": 6, 18, 30, 42, 54
- Overlapping Region (Multiples of 12): 12, 24, 36, 48, 60 (These are already shown)
- Region outside both circles (numbers from 1-60 that are not multiples of 4 or 6): 1, 2, 3, 5, 7, 9, 10, 11, 13, 14, 15, 17, 19, 22, 23, 25, 26, 27, 29, 31, 33, 34, 35, 37, 38, 39, 41, 43, 45, 46, 47, 49, 50, 51, 53, 55, 57, 58, 59. (Listing all 40 numbers).
In the diagram, the labels "Multiples of 4" and "Multiples of 6" should be placed on the respective circles.
Question 9. Find the smallest number that is a multiple of all the numbers from 1 to 10 except for 7.
Answer:
We are looking for the smallest number that is a multiple of all numbers from 1 to 10, except for 7.
This means the number must be a multiple of each number in the set $\{1, 2, 3, 4, 5, 6, 8, 9, 10\}$.
The smallest number that is a multiple of a set of numbers is their Least Common Multiple (LCM).
So, we need to find LCM(1, 2, 3, 4, 5, 6, 8, 9, 10).
To find the LCM, we can use the prime factorization method. Let's list the prime factorization of each number:
- $1 = 1$
- $2 = 2^1$
- $3 = 3^1$
- $4 = 2^2$
- $5 = 5^1$
- $6 = 2 \times 3 = 2^1 \times 3^1$
- $8 = 2 \times 2 \times 2 = 2^3$
- $9 = 3 \times 3 = 3^2$
- $10 = 2 \times 5 = 2^1 \times 5^1$
The prime factors involved are 2, 3, and 5.
To find the LCM, we take the highest power of each prime factor that appears in any of the factorizations:
- Highest power of 2: $2^3$ (from 8)
- Highest power of 3: $3^2$ (from 9)
- Highest power of 5: $5^1$ (from 5 or 10)
Now, we multiply these highest powers together to get the LCM:
$\text{LCM}(1, 2, 3, 4, 5, 6, 8, 9, 10) = 2^3 \times 3^2 \times 5^1$
$= 8 \times 9 \times 5$
$= 72 \times 5$
$= 360$
The smallest number that is a multiple of all the numbers from 1 to 10 except for 7 is 360.
Question 10. Find the smallest number that is a multiple of all the numbers from 1 to 10.
Answer:
We are looking for the smallest number that is a multiple of every number in the set of integers from 1 to 10, inclusive.
This number is the Least Common Multiple (LCM) of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
To find the LCM, we can use the prime factorization method.
Let's find the prime factorization of each number from 1 to 10:
$1 = 1$
$2 = 2^1$
$3 = 3^1$
$4 = 2 \times 2 = 2^2$
$5 = 5^1$
$6 = 2 \times 3 = 2^1 \times 3^1$
$7 = 7^1$
$8 = 2 \times 2 \times 2 = 2^3$
$9 = 3 \times 3 = 3^2$
$10 = 2 \times 5 = 2^1 \times 5^1$
Now, identify all the unique prime factors from these factorizations: 2, 3, 5, and 7.
For each unique prime factor, take the highest power that appears in any of the factorizations:
- The highest power of 2 is $2^3$ (from the number 8).
- The highest power of 3 is $3^2$ (from the number 9).
- The highest power of 5 is $5^1$ (from the numbers 5 and 10).
- The highest power of 7 is $7^1$ (from the number 7).
The LCM is the product of these highest powers:
$\text{LCM}(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) = 2^3 \times 3^2 \times 5^1 \times 7^1$
$= 8 \times 9 \times 5 \times 7$
$= 72 \times 35$
Let's perform the multiplication:
$\begin{array}{cc}& & 7 & 2 \\ \times & & 3 & 5 \\ \hline & 3 & 6 & 0 \\ 2 & 1 & 6 & \times \\ \hline 2 & 5 & 2 & 0 \\ \hline \end{array}$
$= 2520$
The smallest number that is a multiple of all the numbers from 1 to 10 is 2520.
Intext Question (Page 113)
Question: How many prime numbers are there from 21 to 30? How many composite numbers are there from 21 to 30?
Answer:
To answer this, we need to examine each integer from 21 to 30 and determine if it is a prime number or a composite number.
Recall: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A composite number is a natural number greater than 1 that is not prime (meaning it has at least one divisor other than 1 and itself).
Let's check each number in the range [21, 30]:
- 21: Divisors are 1, 3, 7, 21. It has divisors other than 1 and 21. So, 21 is composite.
- 22: Divisors are 1, 2, 11, 22. It has divisors other than 1 and 22. So, 22 is composite.
- 23: Divisors are 1, 23. Its only positive divisors are 1 and itself. So, 23 is prime.
- 24: Divisors include 1, 2, 3, 4, 6, 8, 12, 24. It has divisors other than 1 and 24. So, 24 is composite.
- 25: Divisors are 1, 5, 25. It has divisors other than 1 and 25. So, 25 is composite.
- 26: Divisors are 1, 2, 13, 26. It has divisors other than 1 and 26. So, 26 is composite.
- 27: Divisors are 1, 3, 9, 27. It has divisors other than 1 and 27. So, 27 is composite.
- 28: Divisors include 1, 2, 4, 7, 14, 28. It has divisors other than 1 and 28. So, 28 is composite.
- 29: Divisors are 1, 29. Its only positive divisors are 1 and itself. So, 29 is prime.
- 30: Divisors include 1, 2, 3, 5, 6, 10, 15, 30. It has divisors other than 1 and 30. So, 30 is composite.
Based on this analysis:
The prime numbers from 21 to 30 are 23 and 29.
There are 2 prime numbers from 21 to 30.
The composite numbers from 21 to 30 are 21, 22, 24, 25, 26, 27, 28, and 30.
There are 8 composite numbers from 21 to 30.
Figure it Out (Page 114 - 115)
Question 1. We see that 2 is a prime and also an even number. Is there any other even prime?
Answer:
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
An even number is an integer that is divisible by 2.
The number 2 is even because it is divisible by 2 ($2 \div 2 = 1$).
The factors of 2 are 1 and 2. Since its only positive divisors are 1 and itself, 2 is a prime number.
Now consider any other even number, let's call it $N$.
Since $N$ is an even number and $N > 2$ (because we are looking for *other* even primes), $N$ is divisible by 2.
This means that 2 is a positive divisor of $N$.
Since $N$ is an even number greater than 2, $N$ is greater than 2, and $N$ is divisible by 2, which means 2 is a factor of $N$. Also, $N$ has factors 1 and $N$ itself.
Because $N > 2$ and $N$ is even, $N$ has at least three distinct positive divisors: 1, 2, and $N$ (since $N$ must be greater than 2, $N \neq 2$, and since $N$ is divisible by 2, $2 \neq N$).
For a number to be prime, it must have exactly two distinct positive divisors: 1 and itself.
Any even number greater than 2 has at least three positive divisors (1, 2, and the number itself), and therefore cannot be a prime number.
So, the only even number that is also a prime number is 2.
There is no other even prime number besides 2.
Question 2. Look at the list of primes till 100. What is the smallest difference between two successive primes? What is the largest difference?
Answer:
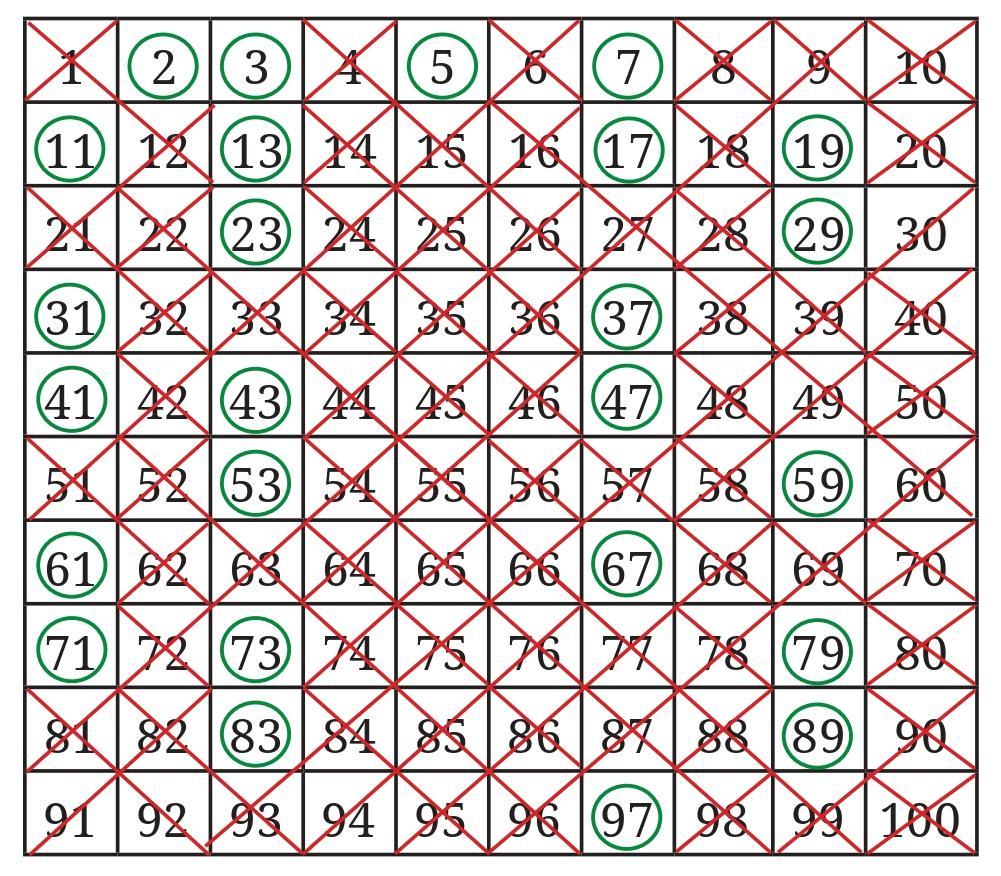
Question 3. Are there an equal number of primes occurring in every row in the table on the previous page? Which decades have the least number of primes? Which have the most number of primes?
Answer:
Let's count the number of prime numbers in each row (decade) of the table on Page 113.
- Row 1 (1-10): Primes are 2, 3, 5, 7. There are 4 primes.
- Row 2 (11-20): Primes are 11, 13, 17, 19. There are 4 primes.
- Row 3 (21-30): Primes are 23, 29. There are 2 primes.
- Row 4 (31-40): Primes are 31, 37. There are 2 primes.
- Row 5 (41-50): Primes are 41, 43, 47. There are 3 primes.
- Row 6 (51-60): Primes are 53, 59. There are 2 primes.
- Row 7 (61-70): Primes are 61, 67. There are 2 primes.
- Row 8 (71-80): Primes are 71, 73, 79. There are 3 primes.
- Row 9 (81-90): Primes are 83, 89. There are 2 primes.
- Row 10 (91-100): Prime is 97. There is 1 prime.
The number of primes in each row are 4, 4, 2, 2, 3, 2, 2, 3, 2, 1.
Are there an equal number of primes occurring in every row in the table?
No, the number of primes per row is not the same for every row. For example, the first row has 4 primes, while the third row has 2 primes.
Which decades have the least number of primes?
The minimum number of primes in a row is 1.
This occurs in the decade 91-100.
The decade with the least number of primes is 91-100.
Which have the most number of primes?
The maximum number of primes in a row is 4.
This occurs in the decades 1-10 and 11-20.
The decades with the most number of primes are 1-10 and 11-20.
Question 4. Which of the following numbers are prime? 23, 51, 37, 26
Answer:
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's examine each number:
23: The positive divisors of 23 are 1 and 23. Since its only positive divisors are 1 and itself, 23 is a prime number.
51: 51 is divisible by 3 and 17. Its positive divisors are 1, 3, 17, and 51. Since it has positive divisors other than 1 and 51 ($51 = 3 \times 17$), 51 is not a prime number.
37: The positive divisors of 37 are 1 and 37. Since its only positive divisors are 1 and itself, 37 is a prime number.
26: 26 is divisible by 2 and 13. Its positive divisors are 1, 2, 13, and 26. Since it has positive divisors other than 1 and 26 ($26 = 2 \times 13$), 26 is not a prime number.
Therefore, the prime numbers from the given list are 23 and 37.
Question 5. Write three pairs of prime numbers less than 20 whose sum is a multiple of 5.
Answer:
First, let's list all the prime numbers less than 20:
2, 3, 5, 7, 11, 13, 17, 19.
We need to find pairs of these numbers such that their sum is a multiple of 5 (i.e., the sum ends in 0 or 5).
Here are three such pairs:
1. The pair (2, 3): Both 2 and 3 are prime numbers less than 20. Their sum is $2 + 3 = 5$. Since 5 is a multiple of 5, this pair satisfies the condition.
2. The pair (3, 7): Both 3 and 7 are prime numbers less than 20. Their sum is $3 + 7 = 10$. Since 10 is a multiple of 5, this pair satisfies the condition.
3. The pair (13, 17): Both 13 and 17 are prime numbers less than 20. Their sum is $13 + 17 = 30$. Since 30 is a multiple of 5, this pair satisfies the condition.
Other possible pairs include (2, 13), (7, 13), (11, 19).
Question 6. The numbers 13 and 31 are prime numbers. Both these numbers have same digits 1 and 3. Find such pairs of prime numbers up to 100.
Answer:
First, let's list the prime numbers up to 100:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
We are looking for pairs of these prime numbers where both numbers in the pair consist of the same digits.
Let's consider the two-digit prime numbers and check if reversing their digits also results in a prime number from the list:
- The digits of 13 are 1 and 3. Reversing gives 31. 31 is also a prime number.
- The digits of 17 are 1 and 7. Reversing gives 71. 71 is also a prime number.
- The digits of 37 are 3 and 7. Reversing gives 73. 73 is also a prime number.
- The digits of 79 are 7 and 9. Reversing gives 97. 97 is also a prime number.
Other two-digit prime numbers (like 23, 29, 41, etc.) do not form such pairs when their digits are reversed and checked against the list of primes up to 100.
The pairs of prime numbers up to 100 that have the same digits are:
1. (13, 31)
2. (17, 71)
3. (37, 73)
4. (79, 97)
Question 7. Find seven consecutive composite numbers between 1 and 100.
Answer:
A composite number is a natural number greater than 1 that is not a prime number. In other words, it has at least one divisor other than 1 and itself.
We are looking for a sequence of seven numbers between 1 and 100 where every number in the sequence is composite.
Let's examine numbers in the range between 1 and 100 to find such a sequence.
Consider the numbers from 90 to 96:
- 90 is composite ($90 = 9 \times 10$)
- 91 is composite ($91 = 7 \times 13$)
- 92 is composite ($92 = 4 \times 23$)
- 93 is composite ($93 = 3 \times 31$)
- 94 is composite ($94 = 2 \times 47$)
- 95 is composite ($95 = 5 \times 19$)
- 96 is composite ($96 = 3 \times 32$)
All these seven numbers are composite, and they are consecutive.
Therefore, seven consecutive composite numbers between 1 and 100 are 90, 91, 92, 93, 94, 95, and 96.
Question 8. Twin primes are pairs of primes having a difference of 2. For example, 3 and 5 are twin primes. So are 17 and 19. Find the other twin primes between 1 and 100.
Answer:
A pair of prime numbers is called twin primes if their difference is 2.
The prime numbers between 1 and 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
We need to find pairs of these prime numbers whose difference is 2. The given examples are (3, 5) and (17, 19).
Let's check the differences between consecutive primes (skipping 2, as $5-2=3$):
$5 - 3 = 2$
$7 - 5 = 2$
$13 - 11 = 2$
$19 - 17 = 2$
$31 - 29 = 2$
$43 - 41 = 2$
$61 - 59 = 2$
$73 - 71 = 2$
Other differences are greater than 2.
The other twin prime pairs between 1 and 100 are:
(5, 7)
(11, 13)
(29, 31)
(41, 43)
(59, 61)
(71, 73)
Question 9. Identify whether each statement is true or false. Explain.
a. There is no prime number whose units digit is 4.
b. A product of primes can also be prime.
c. Prime numbers do not have any factors.
d. All even numbers are composite numbers.
e. 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Answer:
a. There is no prime number whose units digit is 4.
Statement: True.
Explanation: Any number ending in the digit 4 is an even number (except 0). Any even number greater than 2 is divisible by 2, in addition to 1 and itself. This means any even number greater than 2 has at least three positive divisors (1, 2, and the number itself), making it a composite number. The number 2 is the only even prime number, and its units digit is 2, not 4. The number 4 itself is $2 \times 2$, which is composite. Therefore, no prime number can have a units digit of 4.
b. A product of primes can also be prime.
Statement: True.
Explanation: The statement can be interpreted as the product of one or more prime numbers. If we consider the product of a single prime number, say 7, the result is 7, which is a prime number. If the statement implies the product of two or more primes, then the result would always be composite (as it would have the primes themselves as factors, in addition to 1 and the product). However, under the interpretation that allows the product of a single prime, the statement holds true.
c. Prime numbers do not have any factors.
Statement: False.
Explanation: By definition, a prime number is a natural number greater than 1 that has exactly two distinct positive divisors (or factors): 1 and itself. For example, the prime number 5 has factors 1 and 5. The statement is incorrect because prime numbers do have factors, specifically two factors.
d. All even numbers are composite numbers.
Statement: False.
Explanation: An even number is an integer that is divisible by 2. The number 2 is an even number. Its positive divisors are 1 and 2. According to the definition of a prime number, a number greater than 1 with exactly two positive divisors (1 and itself) is prime. Thus, 2 is a prime number. Therefore, not all even numbers are composite numbers, as 2 is a counterexample.
e. 2 is a prime and so is the next number, 3. For every other prime, the next number is composite.
Statement: True.
Explanation: The number 2 is prime. The next integer is 3, which is also prime. This part of the statement is correct. Now, consider any prime number $p$ other than 2 and 3. If $p$ is a prime number greater than 3, it must be an odd number (since 2 is the only even prime). The integer immediately following an odd number $p$ is $p+1$. Since $p$ is odd, $p+1$ must be an even number. Any even number greater than 2 is composite because it is divisible by 2 (and also by 1 and itself). Since we are considering primes $p > 3$, $p+1$ will be an even number greater than 4 ($3+1=4$). Thus, for any prime $p > 3$, the next number $p+1$ is an even number greater than 4, and is therefore composite. The statement is correct.
Question 10. Which of the following numbers is the product of exactly three distinct prime numbers: 45, 60, 91, 105, 330?
Answer:
We need to find the prime factorization of each given number and count the number of distinct prime factors.
Let's factorize each number:
For 45:
$45 = 3 \times 15 = 3 \times 3 \times 5 = 3^2 \times 5$
The distinct prime factors are 3 and 5. There are 2 distinct prime factors.
For 60:
$60 = 2 \times 30 = 2 \times 2 \times 15 = 2 \times 2 \times 3 \times 5 = 2^2 \times 3 \times 5$
The distinct prime factors are 2, 3, and 5. There are 3 distinct prime factors.
For 91:
$91 = 7 \times 13$
The distinct prime factors are 7 and 13. There are 2 distinct prime factors.
For 105:
$105 = 3 \times 35 = 3 \times 5 \times 7$
The distinct prime factors are 3, 5, and 7. There are 3 distinct prime factors.
For 330:
$330 = 10 \times 33 = (2 \times 5) \times (3 \times 11) = 2 \times 3 \times 5 \times 11$
The distinct prime factors are 2, 3, 5, and 11. There are 4 distinct prime factors.
Based on the prime factorizations, the numbers that are the product of exactly three distinct prime numbers are those with exactly three unique prime factors.
The numbers are 60 (distinct prime factors 2, 3, 5) and 105 (distinct prime factors 3, 5, 7).
Therefore, from the given list, the numbers that are the product of exactly three distinct prime numbers are 60 and 105.
Question 11. How many three-digit prime numbers can you make using each of 2, 4 and 5 once?
Answer:
We are asked to find the number of three-digit prime numbers that can be formed using the digits 2, 4, and 5 exactly once.
First, let's list all possible three-digit numbers that can be formed using the digits 2, 4, and 5 exactly once. These are the permutations of the digits:
245, 254, 425, 452, 524, 542.
Now, let's examine the primality of each of these numbers.
We can use divisibility rules to quickly identify if these numbers are composite.
Any integer ending in an even digit (0, 2, 4, 6, 8) is divisible by 2. Any integer ending in 5 is divisible by 5.
Let's check our list:
- 245 ends in 5, so it is divisible by 5. $245 = 5 \times 49$. It is a composite number.
- 254 ends in 4 (an even digit), so it is divisible by 2. $254 = 2 \times 127$. It is a composite number.
- 425 ends in 5, so it is divisible by 5. $425 = 5 \times 85$. It is a composite number.
- 452 ends in 2 (an even digit), so it is divisible by 2. $452 = 2 \times 226$. It is a composite number.
- 524 ends in 4 (an even digit), so it is divisible by 2. $524 = 2 \times 262$. It is a composite number.
- 542 ends in 2 (an even digit), so it is divisible by 2. $542 = 2 \times 271$. It is a composite number.
Alternatively, we can observe that any three-digit number formed using the digits 2, 4, and 5 must end in either 2, 4, or 5.
- If the number ends in 2 or 4, it is an even number greater than 2, so it is divisible by 2 and therefore composite.
- If the number ends in 5, it is divisible by 5. Since these are three-digit numbers, they are greater than 5, so they are divisible by 5 and therefore composite.
Thus, none of the numbers formed using these digits are prime.
Therefore, the number of three-digit prime numbers that can be made using each of 2, 4, and 5 once is 0.
Question 12. Observe that 3 is a prime number, and 2 × 3 + 1 = 7 is also a prime. Are there other primes for which doubling and adding 1 gives another prime? Find at least five such examples.
Answer:
We are looking for prime numbers $p$ such that the number $2p + 1$ is also a prime number.
Let's test some prime numbers starting from the smallest one:
- If $p = 2$ (which is prime), then $2p + 1 = 2(2) + 1 = 4 + 1 = 5$. The number 5 is prime.
So, (2, 5) is such a pair.
- If $p = 3$ (which is prime), then $2p + 1 = 2(3) + 1 = 6 + 1 = 7$. The number 7 is prime. (This example was given in the question).
So, (3, 7) is such a pair.
- If $p = 5$ (which is prime), then $2p + 1 = 2(5) + 1 = 10 + 1 = 11$. The number 11 is prime.
So, (5, 11) is such a pair.
- If $p = 7$ (which is prime), then $2p + 1 = 2(7) + 1 = 14 + 1 = 15$. The number 15 is composite ($15 = 3 \times 5$).
- If $p = 11$ (which is prime), then $2p + 1 = 2(11) + 1 = 22 + 1 = 23$. The number 23 is prime.
So, (11, 23) is such a pair.
- If $p = 13$ (which is prime), then $2p + 1 = 2(13) + 1 = 26 + 1 = 27$. The number 27 is composite ($27 = 3 \times 9$).
- If $p = 17$ (which is prime), then $2p + 1 = 2(17) + 1 = 34 + 1 = 35$. The number 35 is composite ($35 = 5 \times 7$).
- If $p = 19$ (which is prime), then $2p + 1 = 2(19) + 1 = 38 + 1 = 39$. The number 39 is composite ($39 = 3 \times 13$).
- If $p = 23$ (which is prime), then $2p + 1 = 2(23) + 1 = 46 + 1 = 47$. The number 47 is prime.
So, (23, 47) is such a pair.
We have found more than five examples of prime numbers $p$ for which $2p + 1$ is also a prime number. Five such examples are:
1. $p = 2$, $2p + 1 = 5$ (Both 2 and 5 are prime)
2. $p = 3$, $2p + 1 = 7$ (Both 3 and 7 are prime)
3. $p = 5$, $2p + 1 = 11$ (Both 5 and 11 are prime)
4. $p = 11$, $2p + 1 = 23$ (Both 11 and 23 are prime)
5. $p = 23$, $2p + 1 = 47$ (Both 23 and 47 are prime)
Intext Question (Page 116)
Question: Which of the following pairs of numbers are co-prime?
a. 18 and 35
b. 15 and 37
c. 30 and 415
d. 17 and 69
e. 81 and 18
Answer:
Two numbers are called co-prime (or relatively prime) if their greatest common divisor (GCD) is 1. This means they do not share any common positive factors other than 1.
Let's check each pair:
a. 18 and 35
Factors of 18 are 1, 2, 3, 6, 9, 18.
Factors of 35 are 1, 5, 7, 35.
The only common positive factor is 1. So, GCD(18, 35) = 1.
Therefore, 18 and 35 are co-prime.
b. 15 and 37
Factors of 15 are 1, 3, 5, 15.
Factors of 37 are 1, 37 (37 is a prime number).
The only common positive factor is 1. So, GCD(15, 37) = 1.
Therefore, 15 and 37 are co-prime.
c. 30 and 415
Factors of 30 include 1, 2, 3, 5, 6, 10, 15, 30.
Since 415 ends in 5, it is divisible by 5. $415 = 5 \times 83$. Factors of 415 include 1, 5, 83, 415.
Both numbers have 5 as a common factor (in addition to 1). So, GCD(30, 415) $\neq$ 1.
Therefore, 30 and 415 are not co-prime.
d. 17 and 69
Factors of 17 are 1, 17 (17 is a prime number).
Factors of 69 include 1, 3, 23, 69 ($69 = 3 \times 23$).
The only common positive factor is 1. So, GCD(17, 69) = 1.
Therefore, 17 and 69 are co-prime.
e. 81 and 18
Factors of 81 are 1, 3, 9, 27, 81.
Factors of 18 are 1, 2, 3, 6, 9, 18.
Both numbers have common factors 3 and 9 (in addition to 1). The GCD is 9. So, GCD(81, 18) $\neq$ 1.
Therefore, 81 and 18 are not co-prime.
The pairs of numbers that are co-prime are:
a. 18 and 35
b. 15 and 37
d. 17 and 69
Question: While playing the ‘idli-vada’ game with different number pairs, Anshu observed something interesting!
a. Sometimes the first common multiple was the same as the product of the two numbers.
b. At other times the first common multiple was less than the product of the two numbers.
Find examples for each of the above. How is it related to the number pair being co-prime?
Answer:
The 'idli-vada' game likely refers to finding the Least Common Multiple (LCM) of two numbers.
Let's consider two positive integers, $a$ and $b$.
There is a relationship between the product of two numbers, their Least Common Multiple (LCM), and their Greatest Common Divisor (GCD). The relationship is given by the formula:
$\text{Product of } a \text{ and } b = \text{GCD}(a, b) \times \text{LCM}(a, b)$
... (i)
or $a \times b = \text{GCD}(a, b) \times \text{LCM}(a, b)$.
Now let's look at Anshu's observations:
a. Sometimes the first common multiple was the same as the product of the two numbers.
This means $\text{LCM}(a, b) = a \times b$.
From the formula (i), if $\text{LCM}(a, b) = a \times b$, then substituting this into the equation gives:
$a \times b = \text{GCD}(a, b) \times (a \times b)$
Dividing both sides by $a \times b$ (assuming $a$ and $b$ are non-zero), we get:
$1 = \text{GCD}(a, b)$
This happens when the Greatest Common Divisor (GCD) of the two numbers is 1.
Numbers whose GCD is 1 are called co-prime numbers.
Examples:
Consider the numbers 3 and 5.
Product of 3 and 5 = $3 \times 5 = 15$.
Multiples of 3: 3, 6, 9, 12, 15, 18, ...
Multiples of 5: 5, 10, 15, 20, ...
The first common multiple (LCM) of 3 and 5 is 15.
Here, LCM(3, 5) = 15, which is equal to the product $3 \times 5$.
The GCD(3, 5) = 1. The numbers 3 and 5 are co-prime.
Consider the numbers 4 and 7.
Product of 4 and 7 = $4 \times 7 = 28$.
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, ...
Multiples of 7: 7, 14, 21, 28, ...
The first common multiple (LCM) of 4 and 7 is 28.
Here, LCM(4, 7) = 28, which is equal to the product $4 \times 7$.
The GCD(4, 7) = 1. The numbers 4 and 7 are co-prime.
This observation occurs when the two numbers are co-prime.
b. At other times the first common multiple was less than the product of the two numbers.
This means $\text{LCM}(a, b) < a \times b$.
From the formula (i), $a \times b = \text{GCD}(a, b) \times \text{LCM}(a, b)$.
If $\text{LCM}(a, b) < a \times b$, it implies that $\text{GCD}(a, b)$ must be greater than 1.
This happens when the two numbers have a common factor other than 1, meaning they are not co-prime.
Examples:
Consider the numbers 4 and 6.
Product of 4 and 6 = $4 \times 6 = 24$.
Multiples of 4: 4, 8, 12, 16, 20, 24, ...
Multiples of 6: 6, 12, 18, 24, ...
The first common multiple (LCM) of 4 and 6 is 12.
Here, LCM(4, 6) = 12, which is less than the product $4 \times 6 = 24$.
The common factors of 4 and 6 are 1 and 2. The GCD(4, 6) = 2. Since GCD > 1, the numbers 4 and 6 are not co-prime.
Consider the numbers 10 and 15.
Product of 10 and 15 = $10 \times 15 = 150$.
Multiples of 10: 10, 20, 30, 40, ...
Multiples of 15: 15, 30, 45, ...
The first common multiple (LCM) of 10 and 15 is 30.
Here, LCM(10, 15) = 30, which is less than the product $10 \times 15 = 150$.
The common factors of 10 and 15 are 1 and 5. The GCD(10, 15) = 5. Since GCD > 1, the numbers 10 and 15 are not co-prime.
This observation occurs when the two numbers are not co-prime.
Relationship to co-prime numbers:
The first common multiple (LCM) of two numbers is equal to their product if and only if the two numbers are co-prime (their GCD is 1).
The first common multiple (LCM) of two numbers is less than their product if and only if the two numbers are not co-prime (their GCD is greater than 1).
Intext Question (Page 117)
Observe the following thread art. The first diagram has 12 pegs and the thread is tied to every fourth peg (we say that the thread-gap is 4). The second diagram has 13 pegs and the thread-gap is 3. What about the other diagrams? Observe these pictures, share and discuss your findings in class.
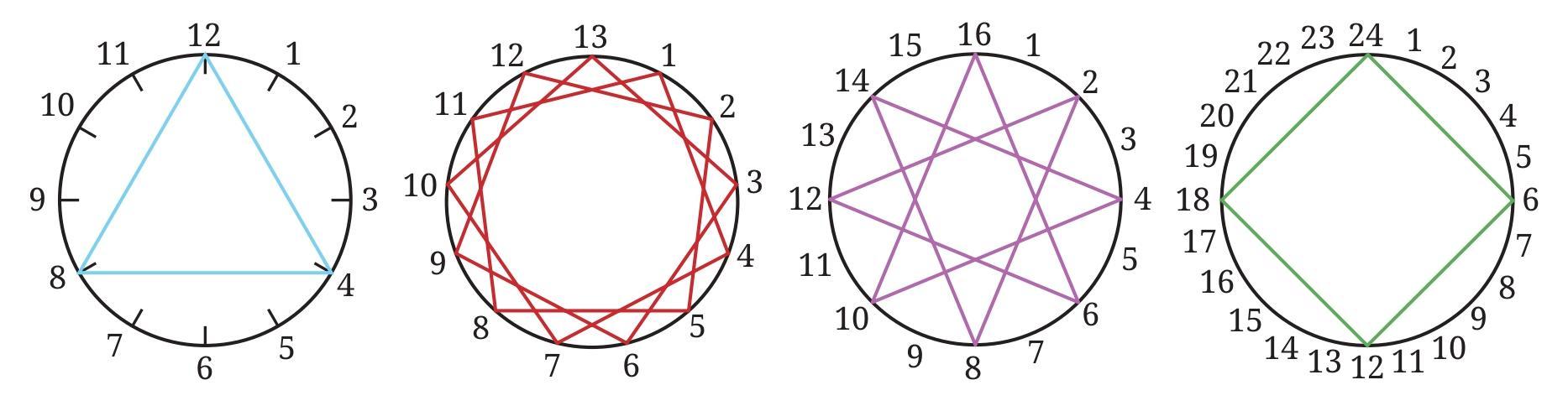
In some diagrams, the thread is tied to every peg. In some, it is not. Is it related to the two numbers (the number of pegs and the thread-gap) being co-prime?
Question: Make such pictures for the following:
a. 15 pegs, thread-gap of 10
b. 10 pegs, thread-gap of 7
c. 14 pegs, thread-gap of 6
d. 8 pegs, thread-gap of 3
Answer:
This problem explores the relationship between the number of pegs, the thread-gap, and whether the thread visits every peg in the thread art. The key concept involved here is the Greatest Common Divisor (GCD) and co-prime numbers.
The thread starts at peg 0 and jumps by the thread-gap amount, wrapping around the circle of pegs. The thread will visit every peg if and only if the number of pegs and the thread-gap are co-prime, which means their Greatest Common Divisor (GCD) is 1.
Let's analyze the given examples:
Diagram 1: 12 pegs, thread-gap 4. GCD(12, 4). Factors of 12: 1, 2, 3, 4, 6, 12. Factors of 4: 1, 2, 4. GCD(12, 4) = 4. Since GCD > 1, 12 and 4 are not co-prime. The thread does not visit every peg (it visits 0, 4, 8).
Diagram 2: 13 pegs, thread-gap 3. GCD(13, 3). Factors of 13: 1, 13. Factors of 3: 1, 3. GCD(13, 3) = 1. Since GCD = 1, 13 and 3 are co-prime. The thread visits every peg.
Now let's determine if the thread visits every peg for the given examples by finding the GCD of the number of pegs and the thread-gap:
a. 15 pegs, thread-gap of 10
We need to find GCD(15, 10).
Factors of 15: 1, 3, 5, 15.
Factors of 10: 1, 2, 5, 10.
The common factors are 1 and 5. The GCD(15, 10) = 5.
Since GCD(15, 10) = 5, which is greater than 1, the numbers 15 and 10 are not co-prime.
Therefore, the thread will not be tied to every peg.
b. 10 pegs, thread-gap of 7
We need to find GCD(10, 7).
Factors of 10: 1, 2, 5, 10.
Factors of 7: 1, 7 (7 is a prime number).
The only common factor is 1. The GCD(10, 7) = 1.
Since GCD(10, 7) = 1, the numbers 10 and 7 are co-prime.
Therefore, the thread will be tied to every peg.
c. 14 pegs, thread-gap of 6
We need to find GCD(14, 6).
Factors of 14: 1, 2, 7, 14.
Factors of 6: 1, 2, 3, 6.
The common factors are 1 and 2. The GCD(14, 6) = 2.
Since GCD(14, 6) = 2, which is greater than 1, the numbers 14 and 6 are not co-prime.
Therefore, the thread will not be tied to every peg.
d. 8 pegs, thread-gap of 3
We need to find GCD(8, 3).
Factors of 8: 1, 2, 4, 8.
Factors of 3: 1, 3 (3 is a prime number).
The only common factor is 1. The GCD(8, 3) = 1.
Since GCD(8, 3) = 1, the numbers 8 and 3 are co-prime.
Therefore, the thread will be tied to every peg.
Summary of Findings:
The thread visits every peg if and only if the number of pegs and the thread-gap are co-prime (i.e., their GCD is 1).
- For 15 pegs and gap 10, GCD = 5. Not co-prime. Thread does not visit every peg.
- For 10 pegs and gap 7, GCD = 1. Co-prime. Thread visits every peg.
- For 14 pegs and gap 6, GCD = 2. Not co-prime. Thread does not visit every peg.
- For 8 pegs and gap 3, GCD = 1. Co-prime. Thread visits every peg.
Figure it Out (Page 120)
Question 1. Find the prime factorisations of the following numbers: 64, 104, 105, 243, 320, 141, 1728, 729, 1024, 1331, 1000.
Answer:
To find the prime factorization of a number, we express it as a product of prime numbers.
The prime factorization of 64 is:
$64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6$
The prime factorization of 104 is:
$104 = 2 \times 2 \times 2 \times 13 = 2^3 \times 13$
The prime factorization of 105 is:
$105 = 3 \times 5 \times 7$
The prime factorization of 243 is:
$243 = 3 \times 3 \times 3 \times 3 \times 3 = 3^5$
The prime factorization of 320 is:
$320 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 = 2^6 \times 5$
The prime factorization of 141 is:
$141 = 3 \times 47$
The prime factorization of 1728 is:
$1728 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^6 \times 3^3$
The prime factorization of 729 is:
$729 = 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 3^6$
The prime factorization of 1024 is:
$1024 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{10}$
The prime factorization of 1331 is:
$1331 = 11 \times 11 \times 11 = 11^3$
The prime factorization of 1000 is:
$1000 = 2 \times 2 \times 2 \times 5 \times 5 \times 5 = 2^3 \times 5^3$
Question 2. The prime factorisation of a number has one 2, two 3s, and one 11. What is the number?
Answer:
The prime factorization of a number expresses it as a product of its prime factors.
We are given that the prime factorization of the number consists of:
- One factor of 2 (which can be written as $2^1$)
- Two factors of 3 (which can be written as $3^2$)
- One factor of 11 (which can be written as $11^1$)
To find the number, we need to multiply these prime factors together:
Number $= 2^1 \times 3^2 \times 11^1$
Number $= 2 \times (3 \times 3) \times 11$
Number $= 2 \times 9 \times 11$
Number $= 18 \times 11$
Performing the multiplication:
$18 \times 11 = 198$
Therefore, the number whose prime factorization is one 2, two 3s, and one 11 is 198.
Question 3. Find three prime numbers, all less than 30, whose product is 1955.
Answer:
We are looking for three distinct prime numbers, each less than 30, whose product is 1955.
To find these numbers, we should find the prime factorization of 1955.
Let's start dividing 1955 by the smallest prime numbers:
- 1955 is not divisible by 2 (it is an odd number).
- The sum of the digits is $1 + 9 + 5 + 5 = 20$. 20 is not divisible by 3, so 1955 is not divisible by 3.
- 1955 ends in 5, so it is divisible by 5.
$1955 \div 5 = 391$
Now we need to find the prime factors of 391.
Let's try dividing 391 by prime numbers greater than 5 (7, 11, 13, 17, 19, 23, ...):
- $391 \div 7 = 55$ with a remainder.
- $391 \div 11 = 35$ with a remainder.
- $391 \div 13 = 30$ with a remainder.
- $391 \div 17 = 23$.
Both 17 and 23 are prime numbers.
So, the prime factorization of 1955 is $5 \times 17 \times 23$.
The three prime numbers are 5, 17, and 23.
Let's check if these numbers satisfy the conditions:
1. Are they prime numbers? Yes, 5, 17, and 23 are all prime numbers.
2. Are they distinct? Yes, they are all different from each other.
3. Are they all less than 30? Yes, $5 < 30$, $17 < 30$, and $23 < 30$.
4. Is their product 1955? $5 \times 17 \times 23 = 85 \times 23 = 1955$. Yes.
The three prime numbers are 5, 17, and 23.
Question 4. Find the prime factorisation of these numbers without multiplying first
a. 56 × 25
b. 108 × 75
c. 1000 × 81
Answer:
To find the prime factorization of a product of numbers without multiplying first, we find the prime factorization of each number separately and then combine the results.
a. $56 \times 25$
First, find the prime factorization of 56:
$56 = 8 \times 7 = (2 \times 2 \times 2) \times 7 = 2^3 \times 7^1$
Next, find the prime factorization of 25:
$25 = 5 \times 5 = 5^2$
The prime factorization of $56 \times 25$ is the product of the prime factorizations of 56 and 25:
$56 \times 25 = (2^3 \times 7^1) \times (5^2)$
Arranging the prime factors in increasing order:
$56 \times 25 = 2^3 \times 5^2 \times 7^1$
b. $108 \times 75$
First, find the prime factorization of 108:
$108 = 2 \times 54 = 2 \times 2 \times 27 = 2 \times 2 \times 3 \times 9 = 2 \times 2 \times 3 \times 3 \times 3 = 2^2 \times 3^3$
Next, find the prime factorization of 75:
$75 = 3 \times 25 = 3 \times 5 \times 5 = 3^1 \times 5^2$
The prime factorization of $108 \times 75$ is the product of the prime factorizations of 108 and 75:
$108 \times 75 = (2^2 \times 3^3) \times (3^1 \times 5^2)$
Combining the powers of the same prime factors ($3^3 \times 3^1 = 3^{3+1} = 3^4$):
$108 \times 75 = 2^2 \times 3^4 \times 5^2$
c. $1000 \times 81$
First, find the prime factorization of 1000:
$1000 = 10 \times 100 = (2 \times 5) \times (10 \times 10) = (2 \times 5) \times (2 \times 5) \times (2 \times 5) = 2 \times 2 \times 2 \times 5 \times 5 \times 5 = 2^3 \times 5^3$
Next, find the prime factorization of 81:
$81 = 9 \times 9 = (3 \times 3) \times (3 \times 3) = 3^4$
The prime factorization of $1000 \times 81$ is the product of the prime factorizations of 1000 and 81:
$1000 \times 81 = (2^3 \times 5^3) \times (3^4)$
Arranging the prime factors in increasing order:
$1000 \times 81 = 2^3 \times 3^4 \times 5^3$
Question 5. What is the smallest number whose prime factorisation has:
a. three different prime numbers?
b. four different prime numbers?
Answer:
To find the smallest number whose prime factorization has a given number of distinct prime factors, we should use the smallest prime numbers and multiply them together. Each distinct prime factor must appear at least once, so the lowest power for each distinct prime will be 1.
a. three different prime numbers
We need to use the three smallest distinct prime numbers. These are 2, 3, and 5.
The smallest number with these three distinct prime factors is the product of these primes raised to the power of 1:
Smallest number $= 2 \times 3 \times 5$
Smallest number $= 6 \times 5$
Smallest number $= 30$
b. four different prime numbers
We need to use the four smallest distinct prime numbers. These are 2, 3, 5, and 7.
The smallest number with these four distinct prime factors is the product of these primes raised to the power of 1:
Smallest number $= 2 \times 3 \times 5 \times 7$
Smallest number $= 6 \times 5 \times 7$
Smallest number $= 30 \times 7$
Smallest number $= 210$
Figure it Out (Page 122)
Question 1. Are the following pairs of numbers co-prime? Guess first and then use prime factorisation to verify your answer.
a. 30 and 45
b. 57 and 85
c. 121 and 1331
d. 343 and 216
Answer:
Two numbers are co-prime if their Greatest Common Divisor (GCD) is 1. We can verify this by finding the prime factorization of each number and checking for common prime factors.
a. 30 and 45
Guess: Both numbers end in 0 or 5, so they are divisible by 5. Thus, they are likely not co-prime.
Prime Factorization:
Prime factors of 30: $30 = 2 \times 15 = 2 \times 3 \times 5$
Prime factors of 45: $45 = 5 \times 9 = 5 \times 3 \times 3 = 3^2 \times 5$
Verification: The common prime factors are 3 and 5. The GCD is $3 \times 5 = 15$. Since GCD(30, 45) = 15, which is not 1, the numbers are not co-prime.
Result: 30 and 45 are not co-prime.
b. 57 and 85
Guess: Not immediately obvious if they share factors other than 1.
Prime Factorization:
Prime factors of 57: $57 = 3 \times 19$ (Since $5+7=12$, which is divisible by 3. 19 is prime).
Prime factors of 85: $85 = 5 \times 17$ (Since it ends in 5. 17 is prime).
Verification: The prime factors of 57 are 3 and 19. The prime factors of 85 are 5 and 17. There are no common prime factors.
Since there are no common prime factors, the GCD is 1. GCD(57, 85) = 1.
Result: 57 and 85 are co-prime.
c. 121 and 1331
Guess: 121 is $11 \times 11$. Let's check if 1331 is related to 11.
Prime Factorization:
Prime factors of 121: $121 = 11 \times 11 = 11^2$ (11 is prime).
Prime factors of 1331: $1331 = 11 \times 121 = 11 \times 11 \times 11 = 11^3$ (11 is prime).
Verification: The common prime factor is 11. The GCD is 11.
Since GCD(121, 1331) = 11, which is not 1, the numbers are not co-prime.
Result: 121 and 1331 are not co-prime.
d. 343 and 216
Guess: 343 might be $7^3$. 216 is $6^3$, which involves factors 2 and 3. They seem unrelated.
Prime Factorization:
Prime factors of 343: $343 = 7 \times 49 = 7 \times 7 \times 7 = 7^3$ (7 is prime).
Prime factors of 216: $216 = 6 \times 36 = (2 \times 3) \times (6 \times 6) = (2 \times 3) \times (2 \times 3) \times (2 \times 3) = 2 \times 2 \times 2 \times 3 \times 3 \times 3 = 2^3 \times 3^3$ (2 and 3 are prime).
Verification: The prime factors of 343 are only 7. The prime factors of 216 are only 2 and 3. There are no common prime factors.
Since there are no common prime factors, the GCD is 1. GCD(343, 216) = 1.
Result: 343 and 216 are co-prime.
Question 2. Is the first number divisible by the second? Use prime factorisation.
a. 225 and 27
b. 96 and 24
c. 343 and 17
d. 999 and 99
Answer:
To determine if a number $A$ is divisible by a number $B$ using prime factorization, we find the prime factorization of both $A$ and $B$. If $A$ is divisible by $B$, then every prime factor in the factorization of $B$ must also be a prime factor in the factorization of $A$, and the exponent of each prime factor in $A$ must be greater than or equal to its exponent in $B$.
a. 225 and 27
Prime factorization of 225: $225 = 3 \times 75 = 3 \times 3 \times 25 = 3^2 \times 5^2$
Prime factorization of 27: $27 = 3 \times 9 = 3 \times 3 \times 3 = 3^3$
For 225 to be divisible by 27, the prime factor 3 in the factorization of 225 must have an exponent of at least 3 (the exponent of 3 in the factorization of 27). However, the exponent of 3 in 225 is 2, which is less than 3.
Therefore, 225 is not divisible by 27.
b. 96 and 24
Prime factorization of 96: $96 = 2 \times 48 = 2 \times 2 \times 24 = 2 \times 2 \times 2 \times 12 = 2 \times 2 \times 2 \times 2 \times 6 = 2 \times 2 \times 2 \times 2 \times 2 \times 3 = 2^5 \times 3^1$
Prime factorization of 24: $24 = 2 \times 12 = 2 \times 2 \times 6 = 2 \times 2 \times 2 \times 3 = 2^3 \times 3^1$
Comparing the prime factors and their exponents:
- Prime factor 2: Exponent in 96 is 5, exponent in 24 is 3. $5 \geq 3$.
- Prime factor 3: Exponent in 96 is 1, exponent in 24 is 1. $1 \geq 1$.
Since all prime factors of 24 are present in 96 with exponents greater than or equal to their exponents in 24, 96 is divisible by 24.
Therefore, 96 is divisible by 24.
c. 343 and 17
Prime factorization of 343: $343 = 7 \times 49 = 7 \times 7 \times 7 = 7^3$ (7 is prime).
Prime factorization of 17: 17 (17 is a prime number).
For 343 to be divisible by 17, the prime factor 17 must be present in the prime factorization of 343. The prime factorization of 343 only contains the prime factor 7.
Therefore, 343 is not divisible by 17.
d. 999 and 99
Prime factorization of 999: $999 = 9 \times 111 = (3 \times 3) \times (3 \times 37) = 3^3 \times 37^1$ (37 is prime).
Prime factorization of 99: $99 = 9 \times 11 = (3 \times 3) \times 11 = 3^2 \times 11^1$ (11 is prime).
Comparing the prime factors and their exponents:
- Prime factor 3: Exponent in 999 is 3, exponent in 99 is 2. $3 \geq 2$.
- Prime factor 11: Exponent in 999 is 0 (not present), exponent in 99 is 1. $0 < 1$.
Since the prime factor 11 is present in 99 but not in 999, 999 is not divisible by 99.
Therefore, 999 is not divisible by 99.
Question 3. The first number has prime factorisation 2 × 3 × 7 and the second number has prime factorisation 3 × 7 × 11. Are they co-prime? Does one of them divide the other?
Answer:
Let the first number be $N_1$ and the second number be $N_2$.
The prime factorization of $N_1$ is $2 \times 3 \times 7$.
The prime factorization of $N_2$ is $3 \times 7 \times 11$.
Are they co-prime?
Two numbers are co-prime if their Greatest Common Divisor (GCD) is 1.
To find the GCD using prime factorization, we identify the common prime factors and multiply them, using the lowest power of each common factor.
Prime factors of $N_1$: 2, 3, 7.
Prime factors of $N_2$: 3, 7, 11.
The common prime factors are 3 and 7.
GCD($N_1$, $N_2$) $= 3 \times 7 = 21$.
Since the GCD is 21 (which is not 1), the numbers $N_1$ and $N_2$ are not co-prime.
Does one of them divide the other?
A number $A$ is divisible by a number $B$ if all prime factors of $B$ are present in the prime factorization of $A$, with their exponents in $A$ being greater than or equal to their exponents in $B$.
Let's check if $N_1$ divides $N_2$:
Prime factors of $N_1$ are 2, 3, 7.
Prime factors of $N_2$ are 3, 7, 11.
The prime factor 2 is present in $N_1$ but not in $N_2$. Therefore, $N_1$ does not divide $N_2$.
Let's check if $N_2$ divides $N_1$:
Prime factors of $N_2$ are 3, 7, 11.
Prime factors of $N_1$ are 2, 3, 7.
The prime factor 11 is present in $N_2$ but not in $N_1$. Therefore, $N_2$ does not divide $N_1$.
Neither of the numbers divides the other.
Question 4. Guna says, “Any two prime numbers are co-prime”. Is he right?
Answer:
Guna says, “Any two prime numbers are co-prime”.
Let's consider the definition of co-prime numbers. Two numbers are co-prime if their only common positive factor is 1. Their Greatest Common Divisor (GCD) is 1.
Let $p$ and $q$ be two prime numbers. By definition, a prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and the number itself.
So, the positive divisors of $p$ are $\{1, p\}$.
The positive divisors of $q$ are $\{1, q\}$.
If $p$ and $q$ are distinct prime numbers (meaning $p \neq q$), then their only common positive divisor is 1.
For example, take the prime numbers 5 and 7. Divisors of 5 are {1, 5}. Divisors of 7 are {1, 7}. The only common divisor is 1. GCD(5, 7) = 1.
Another example, prime numbers 13 and 29. Divisors of 13 are {1, 13}. Divisors of 29 are {1, 29}. The only common divisor is 1. GCD(13, 29) = 1.
In general, if $p$ and $q$ are distinct primes, their only common factor is 1.
Therefore, any two distinct prime numbers are co-prime.
Based on the standard mathematical interpretation of "any two prime numbers" referring to two potentially different prime numbers, Guna's statement is right.
Figure it Out (Page 125 - 126)
Question 1. 2024 is a leap year (as February has 29 days). Leap years occur in the years that are multiples of 4, except for those years that are evenly divisible by 100 but not 400.
a. From the year you were born till now, which years were leap years?
b. From the year 2024 till 2099, how many leap years are there?
Answer:
The rules for determining a leap year are:
1. A year is a leap year if it is divisible by 4.
2. However, if a year is divisible by 100, it is not a leap year, unless...
3. ...it is also divisible by 400, in which case it is a leap year.
a. From the year you were born till now, which years were leap years?
As an AI, I do not have a birth year. To determine the leap years from the year you were born until the current year, you need to apply the rules above to each year in that range.
Start with the year you were born and check each subsequent year up to the current year (2024).
For each year, check the following conditions:
- Is the year divisible by 4? If not, it's not a leap year.
- If it is divisible by 4, is it also divisible by 100? If not, it is a leap year.
- If it is divisible by both 4 and 100, is it also divisible by 400? If yes, it is a leap year. If no, it is not a leap year.
For example, if you were born in 2001:
- 2004: divisible by 4, not by 100 $\implies$ Leap year.
- 2008: divisible by 4, not by 100 $\implies$ Leap year.
- 2012: divisible by 4, not by 100 $\implies$ Leap year.
- 2016: divisible by 4, not by 100 $\implies$ Leap year.
- 2020: divisible by 4, not by 100 $\implies$ Leap year.
- 2024: divisible by 4, not by 100 $\implies$ Leap year.
In this example, the leap years between 2001 and 2024 (inclusive) are 2004, 2008, 2012, 2016, 2020, and 2024.
b. From the year 2024 till 2099, how many leap years are there?
We need to count the leap years in the range [2024, 2099]. We apply the leap year rules to each year in this range.
1. Check for years divisible by 4:
The years are 2024, 2028, 2032, ..., 2096.
These are of the form $4 \times n$. The smallest $n$ is $2024 \div 4 = 506$. The largest $n$ such that $4 \times n \leq 2099$ is $n = \lfloor 2099 / 4 \rfloor = 524$.
The values of $n$ range from 506 to 524, inclusive.
The number of such years is $524 - 506 + 1 = 19$.
So, there are 19 years in this range that are divisible by 4.
2. Check for exceptions (years divisible by 100 but not 400):
Are there any years in the range [2024, 2099] that are divisible by 100? The multiples of 100 around this range are 2000, 2100, 2200, etc. None of these fall within the range [2024, 2099].
Since no year in this range is divisible by 100, the exception condition "divisible by 100 but not 400" does not apply to any year in the range [2024, 2099].
3. Check for the override (years divisible by 400):
Are there any years in the range [2024, 2099] that are divisible by 400? The multiples of 400 around this range are ..., 2000, 2400, ... None of these fall within the range [2024, 2099].
Since no year in this range is divisible by 400, the override condition does not apply.
Therefore, for the years from 2024 to 2099, the leap years are exactly those years that are divisible by 4.
We calculated that there are 19 such years.
The leap years are 2024, 2028, 2032, 2036, 2040, 2044, 2048, 2052, 2056, 2060, 2064, 2068, 2072, 2076, 2080, 2084, 2088, 2092, and 2096.
There are 19 leap years from 2024 till 2099.
Question 2. Find the largest and smallest 4-digit numbers that are divisible by 4 and are also palindromes.
Answer:
A 4-digit number that is a palindrome has the form $ABBA$, where $A$ is the thousands digit (and units digit) and $B$ is the hundreds digit (and tens digit).
For a 4-digit number $ABBA$, $A$ must be a digit from 1 to 9, and $B$ must be a digit from 0 to 9.
The value of the number $ABBA$ can be written as $1000A + 100B + 10B + A = 1001A + 110B$.
A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
For a 4-digit palindrome $ABBA$, the last two digits are $BB$. The number formed by the last two digits is $10B + A$. This is incorrect for $ABBA$, the last two digits are the tens digit $B$ and the units digit $A$. So the number formed by the last two digits is $10B + A$.
However, the divisibility rule for 4 can be applied directly to the number $1001A + 110B$.
$1001A + 110B = (1000A + A) + (108B + 2B) = 1000A + 108B + A + 2B$.
Since $1000A$ is divisible by 4 (because 1000 is divisible by 4) and $108B$ is divisible by 4 (because 108 is divisible by 4), the entire number $1001A + 110B$ is divisible by 4 if and only if the remaining part, $A + 2B$, is divisible by 4.
So, we are looking for 4-digit palindromes $ABBA$ such that $A+2B$ is divisible by 4, where $A \in \{1, 2, \dots, 9\}$ and $B \in \{0, 1, \dots, 9\}$.
Finding the Largest 4-digit Palindrome Divisible by 4:
To find the largest number $ABBA$, we should maximize the thousands digit $A$ first, then the hundreds digit $B$.
Let's try the largest possible values for $A$, starting from 9.
Case 1: $A=9$. We need $9 + 2B$ to be divisible by 4. Let's test values for $B$ from 9 down to 0:
- If $B=9$, $9 + 2(9) = 9 + 18 = 27$. 27 is not divisible by 4.
- If $B=8$, $9 + 2(8) = 9 + 16 = 25$. 25 is not divisible by 4.
- If $B=7$, $9 + 2(7) = 9 + 14 = 23$. 23 is not divisible by 4.
- If $B=6$, $9 + 2(6) = 9 + 12 = 21$. 21 is not divisible by 4.
- If $B=5$, $9 + 2(5) = 9 + 10 = 19$. 19 is not divisible by 4.
- If $B=4$, $9 + 2(4) = 9 + 8 = 17$. 17 is not divisible by 4.
- If $B=3$, $9 + 2(3) = 9 + 6 = 15$. 15 is not divisible by 4.
- If $B=2$, $9 + 2(2) = 9 + 4 = 13$. 13 is not divisible by 4.
- If $B=1$, $9 + 2(1) = 9 + 2 = 11$. 11 is not divisible by 4.
- If $B=0$, $9 + 2(0) = 9 + 0 = 9$. 9 is not divisible by 4.
So, there is no 4-digit palindrome starting with 9 that is divisible by 4.
Case 2: $A=8$. We need $8 + 2B$ to be divisible by 4. $8 + 2B = 2(4+B)$. For this to be divisible by 4, $4+B$ must be even, which means $B$ must be an even digit.
Possible even values for $B$ are 8, 6, 4, 2, 0. To maximize the number $8BB8$, we choose the largest possible $B$, which is 8.
If $A=8$ and $B=8$, the number is 8888. Let's check $A+2B = 8 + 2(8) = 8 + 16 = 24$. 24 is divisible by 4 ($24 \div 4 = 6$).
So, 8888 is a palindrome divisible by 4.
Since we started with the largest possible $A$ and moved downwards, and the largest value of $A$ that works is 8, with the largest possible corresponding $B$, the largest number is 8888.
The largest 4-digit palindrome divisible by 4 is 8888.
Finding the Smallest 4-digit Palindrome Divisible by 4:
To find the smallest number $ABBA$, we should minimize the thousands digit $A$ first, then the hundreds digit $B$.
Let's try the smallest possible values for $A$, starting from 1 (since it's a 4-digit number, $A \neq 0$).
Case 1: $A=1$. We need $1 + 2B$ to be divisible by 4. Let's test values for $B$ from 0 up to 9:
- If $B=0$, $1 + 2(0) = 1$. 1 is not divisible by 4.
- If $B=1$, $1 + 2(1) = 3$. 3 is not divisible by 4.
- If $B=2$, $1 + 2(2) = 5$. 5 is not divisible by 4.
- If $B=3$, $1 + 2(3) = 7$. 7 is not divisible by 4.
- If $B=4$, $1 + 2(4) = 9$. 9 is not divisible by 4.
- If $B=5$, $1 + 2(5) = 11$. 11 is not divisible by 4.
- If $B=6$, $1 + 2(6) = 13$. 13 is not divisible by 4.
- If $B=7$, $1 + 2(7) = 15$. 15 is not divisible by 4.
- If $B=8$, $1 + 2(8) = 17$. 17 is not divisible by 4.
- If $B=9$, $1 + 2(9) = 19$. 19 is not divisible by 4.
So, there is no 4-digit palindrome starting with 1 that is divisible by 4.
Case 2: $A=2$. We need $2 + 2B$ to be divisible by 4. $2 + 2B = 2(1+B)$. For this to be divisible by 4, $1+B$ must be even, which means $B$ must be an odd digit.
Possible odd values for $B$ are 1, 3, 5, 7, 9. To minimize the number $2BB2$, we choose the smallest possible $B$, which is 1.
If $A=2$ and $B=1$, the number is 2112. Let's check $A+2B = 2 + 2(1) = 2 + 2 = 4$. 4 is divisible by 4 ($4 \div 4 = 1$).
So, 2112 is a palindrome divisible by 4.
Since we started with the smallest possible $A$ and moved upwards, and the smallest value of $A$ that works is 2, with the smallest possible corresponding $B$, the smallest number is 2112.
The smallest 4-digit palindrome divisible by 4 is 2112.
Question 3. Explore and find out if each statement is always true, sometimes true or never true. You can give examples to support your reasoning.
a. Sum of two even numbers gives a multiple of 4.
b. Sum of two odd numbers gives a multiple of 4.
Answer:
Let's analyze each statement:
a. Sum of two even numbers gives a multiple of 4.
Statement: Sometimes true.
Explanation: An even number can be written in the form $2k$, where $k$ is an integer. Let the two even numbers be $2m$ and $2n$, where $m$ and $n$ are integers.
Their sum is $(2m) + (2n) = 2(m+n)$.
For this sum to be a multiple of 4, $2(m+n)$ must be divisible by 4, which means $m+n$ must be an even number (divisible by 2).
$m+n$ is even if $m$ and $n$ have the same parity (both even or both odd).
Since $m$ and $n$ can be any integers, $m+n$ is not always even.
Examples:
- Consider the even numbers 2 and 4. Their sum is $2 + 4 = 6$. 6 is not a multiple of 4. (Here $m=1$, $n=2$; $m+n=3$ is odd).
- Consider the even numbers 4 and 8. Their sum is $4 + 8 = 12$. 12 is a multiple of 4. (Here $m=2$, $n=4$; $m+n=6$ is even).
Since the sum is sometimes a multiple of 4 and sometimes not, the statement is sometimes true.
b. Sum of two odd numbers gives a multiple of 4.
Statement: Sometimes true.
Explanation: An odd number can be written in the form $2k+1$, where $k$ is an integer. Let the two odd numbers be $2m+1$ and $2n+1$, where $m$ and $n$ are integers.
Their sum is $(2m+1) + (2n+1) = 2m + 2n + 2 = 2(m+n+1)$.
For this sum to be a multiple of 4, $2(m+n+1)$ must be divisible by 4, which means $m+n+1$ must be an even number (divisible by 2).
$m+n+1$ is even if $m+n$ is an odd number.
$m+n$ is odd if $m$ and $n$ have different parity (one is even and the other is odd).
Since $m$ and $n$ can be any integers, $m+n$ is not always odd.
Examples:
- Consider the odd numbers 3 and 5. Their sum is $3 + 5 = 8$. 8 is a multiple of 4. (Here, if $3 = 2(1)+1$, $m=1$ (odd). If $5 = 2(2)+1$, $n=2$ (even). $m$ and $n$ have different parity, so $m+n=3$ is odd, and $m+n+1=4$ is even. $2 \times 4 = 8$ is a multiple of 4).
- Consider the odd numbers 3 and 7. Their sum is $3 + 7 = 10$. 10 is not a multiple of 4. (Here, if $3 = 2(1)+1$, $m=1$ (odd). If $7 = 2(3)+1$, $n=3$ (odd). $m$ and $n$ have the same parity, so $m+n=4$ is even, and $m+n+1=5$ is odd. $2 \times 5 = 10$ is not a multiple of 4).
Since the sum is sometimes a multiple of 4 and sometimes not, the statement is sometimes true.
Question 4. Find the remainders obtained when each of the following numbers are divided by (i) 10, (ii) 5, (iii) 2.
78, 99, 173, 572, 980, 1111, 2345
Answer:
To find the remainder when a number is divided by 10, 5, or 2, we can look at the units digit of the number.
(i) Remainders when divided by 10:
The remainder when a number is divided by 10 is its units digit.
- For 78, the units digit is 8. The remainder is 8.
- For 99, the units digit is 9. The remainder is 9.
- For 173, the units digit is 3. The remainder is 3.
- For 572, the units digit is 2. The remainder is 2.
- For 980, the units digit is 0. The remainder is 0.
- For 1111, the units digit is 1. The remainder is 1.
- For 2345, the units digit is 5. The remainder is 5.
(ii) Remainders when divided by 5:
The remainder when a number is divided by 5 is the remainder obtained when its units digit is divided by 5.
- For 78, the units digit is 8. $8 \div 5$ gives a remainder of 3.
- For 99, the units digit is 9. $9 \div 5$ gives a remainder of 4.
- For 173, the units digit is 3. $3 \div 5$ gives a remainder of 3.
- For 572, the units digit is 2. $2 \div 5$ gives a remainder of 2.
- For 980, the units digit is 0. $0 \div 5$ gives a remainder of 0.
- For 1111, the units digit is 1. $1 \div 5$ gives a remainder of 1.
- For 2345, the units digit is 5. $5 \div 5$ gives a remainder of 0.
(iii) Remainders when divided by 2:
The remainder when a number is divided by 2 is 0 if the number is even, and 1 if the number is odd. We check the units digit: even if units digit is 0, 2, 4, 6, 8; odd if units digit is 1, 3, 5, 7, 9.
- For 78, the units digit is 8 (even). The remainder is 0.
- For 99, the units digit is 9 (odd). The remainder is 1.
- For 173, the units digit is 3 (odd). The remainder is 1.
- For 572, the units digit is 2 (even). The remainder is 0.
- For 980, the units digit is 0 (even). The remainder is 0.
- For 1111, the units digit is 1 (odd). The remainder is 1.
- For 2345, the units digit is 5 (odd). The remainder is 1.
Question 5. The teacher asked if 14560 is divisible by all of 2, 4, 5, 8 and 10. Guna checked for divisibility of 14560 by only two of these numbers and then declared that it was also divisible by all of them. What could those two numbers be?
Answer:
The problem states that Guna checked the divisibility of 14560 by only two numbers from the list {2, 4, 5, 8, 10} and was able to conclude that the number is divisible by all five numbers.
Recall the divisibility rules for these numbers:
- A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8).
- A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
- A number is divisible by 5 if its last digit is 0 or 5.
- A number is divisible by 8 if the number formed by its last three digits is divisible by 8.
- A number is divisible by 10 if its last digit is 0.
We know that if a number is divisible by two numbers, say $N_1$ and $N_2$, it is also divisible by their Least Common Multiple (LCM), provided $N_1$ and $N_2$ are co-prime. More generally, a number divisible by $N_1$ and $N_2$ is divisible by $\text{LCM}(N_1, N_2)$.
For Guna to conclude that 14560 is divisible by {2, 4, 5, 8, 10} by checking only two numbers from this set, the LCM of those two numbers must be a multiple of the LCM of all five numbers.
Let's find the LCM of the set {2, 4, 5, 8, 10}.
The prime factors involved are 2 and 5.
Highest power of 2 in the set is $2^3$ (from 8).
Highest power of 5 in the set is $5^1$ (from 5 and 10).
LCM(2, 4, 5, 8, 10) $= 2^3 \times 5^1 = 8 \times 5 = 40$.
Guna must have checked divisibility by two numbers, $N_1$ and $N_2$, from the set {2, 4, 5, 8, 10} such that if a number is divisible by $N_1$ and $N_2$, it is divisible by 40. This implies that $\text{LCM}(N_1, N_2)$ must be a multiple of 40. Since $N_1$ and $N_2$ are from the set whose LCM is 40, the LCM of $N_1$ and $N_2$ cannot exceed 40. Therefore, we are looking for a pair $(N_1, N_2)$ from the set {2, 4, 5, 8, 10} such that $\text{LCM}(N_1, N_2) = 40$.
Let's check pairs from the given set:
- $\text{LCM}(2, 4) = 4$
- $\text{LCM}(2, 5) = 10$ (Divisibility by 2 and 5 implies divisibility by 10, but not necessarily by 4 or 8. E.g., 10 is div by 2 and 5 but not by 4 or 8).
- $\text{LCM}(2, 8) = 8$
- $\text{LCM}(2, 10) = 10$
- $\text{LCM}(4, 5) = 20$ (Divisibility by 4 and 5 implies divisibility by 20, which covers 2, 4, 5, 10, but not necessarily 8. E.g., 20 is div by 4 and 5 but not by 8).
- $\text{LCM}(4, 8) = 8$
- $\text{LCM}(4, 10) = 20$
- $\text{LCM}(5, 8) = 40$. If a number is divisible by 5 and 8, it is divisible by their LCM, 40. Any number divisible by 40 is also divisible by its factors: 1, 2, 4, 5, 8, 10, 20, 40. This set includes {2, 4, 5, 8, 10}. So, checking divisibility by 5 and 8 is sufficient.
- $\text{LCM}(5, 10) = 10$
- $\text{LCM}(8, 10) = 40$. If a number is divisible by 8 and 10, it is divisible by their LCM, 40. Any number divisible by 40 is also divisible by its factors, including {2, 4, 5, 8, 10}. So, checking divisibility by 8 and 10 is sufficient.
The pairs of numbers from the set {2, 4, 5, 8, 10} whose LCM is 40 are (5, 8) and (8, 10).
If Guna checked divisibility by 5 and 8, and found that 14560 is divisible by both, he could conclude it is divisible by their LCM, 40. Since all numbers {2, 4, 5, 8, 10} are factors of 40, divisibility by 40 implies divisibility by all of them.
If Guna checked divisibility by 8 and 10, and found that 14560 is divisible by both, he could conclude it is divisible by their LCM, 40. Again, since all numbers {2, 4, 5, 8, 10} are factors of 40, divisibility by 40 implies divisibility by all of them.
Therefore, the two numbers Guna checked could be 5 and 8 or 8 and 10.
Question 6. Which of the following numbers are divisible by all of 2, 4, 5, 8 and 10: 572, 2352, 5600, 6000, 77622160.
Answer:
For a number to be divisible by all of 2, 4, 5, 8, and 10, it must be divisible by the Least Common Multiple (LCM) of these numbers.
As determined previously, the LCM of 2, 4, 5, 8, and 10 is 40.
So, we need to check which of the given numbers are divisible by 40.
A number is divisible by 40 if it is divisible by both 5 and 8 (since GCD(5, 8) = 1).
Divisibility Rule for 5: A number is divisible by 5 if its units digit is 0 or 5.
Divisibility Rule for 8: A number is divisible by 8 if the number formed by its last three digits is divisible by 8.
Let's check each number:
572:
- Units digit is 2. Not divisible by 5.
Since it is not divisible by 5, it is not divisible by 40.
2352:
- Units digit is 2. Not divisible by 5.
Since it is not divisible by 5, it is not divisible by 40.
5600:
- Units digit is 0. Divisible by 5.
- The number formed by the last three digits is 600. Is 600 divisible by 8?
$600 \div 8 = 75$. Yes, 600 is divisible by 8.
Since 5600 is divisible by both 5 and 8, it is divisible by 40.
6000:
- Units digit is 0. Divisible by 5.
- The number formed by the last three digits is 000. Is 000 divisible by 8?
$0 \div 8 = 0$. Yes, 000 is divisible by 8.
Since 6000 is divisible by both 5 and 8, it is divisible by 40.
77622160:
- Units digit is 0. Divisible by 5.
- The number formed by the last three digits is 160. Is 160 divisible by 8?
$160 \div 8 = 20$. Yes, 160 is divisible by 8.
Since 77622160 is divisible by both 5 and 8, it is divisible by 40.
The numbers that are divisible by all of 2, 4, 5, 8, and 10 are those that are divisible by 40.
From the list, these numbers are 5600, 6000, and 77622160.
Question 7. Write two numbers whose product is 10000. The two numbers should not have 0 as the units digit.
Answer:
Let the two numbers be $A$ and $B$. We are given that their product is 10000, so $A \times B = 10000$.
We are also given that the units digit of $A$ is not 0, and the units digit of $B$ is not 0.
First, let's find the prime factorization of 10000.
$10000 = 10 \times 1000 = (2 \times 5) \times 1000$
$1000 = 10 \times 100 = (2 \times 5) \times (10 \times 10) = (2 \times 5) \times (2 \times 5) \times (2 \times 5)$
So, $10000 = (2 \times 5) \times (2 \times 5) \times (2 \times 5) \times (2 \times 5)$
$10000 = 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5 = 2^4 \times 5^4$
Any number whose units digit is 0 must be divisible by 10. A number is divisible by 10 if and only if its prime factorization contains at least one factor of 2 and at least one factor of 5.
Since neither $A$ nor $B$ has a units digit of 0, neither $A$ nor $B$ is divisible by 10.
This means the prime factorization of $A$ cannot contain both a factor of 2 and a factor of 5. Similarly, the prime factorization of $B$ cannot contain both a factor of 2 and a factor of 5.
Let the prime factorization of $A$ be $2^a \times 5^b$ and the prime factorization of $B$ be $2^c \times 5^d$.
Since $A \times B = 10000 = 2^4 \times 5^4$, we must have:
$a + c = 4$
... (i)
$b + d = 4$
... (ii)
where $a, b, c, d$ are non-negative integers.
The condition that $A$ does not have a units digit of 0 means $A$ is not divisible by 10. So, its prime factorization $2^a \times 5^b$ cannot have both $a \geq 1$ and $b \geq 1$. This implies either $a=0$ or $b=0$.
The condition that $B$ does not have a units digit of 0 means $B$ is not divisible by 10. So, its prime factorization $2^c \times 5^d$ cannot have both $c \geq 1$ and $d \geq 1$. This implies either $c=0$ or $d=0$.}
So, we must satisfy (either $a=0$ or $b=0$) AND (either $c=0$ or $d=0$).
Consider the possibilities:
Case 1: $a=0$. From (i), $c = 4 - a = 4 - 0 = 4$. Now we need (either $c=0$ or $d=0$). Since $c=4 \neq 0$, we must have $d=0$. From (ii), $b = 4 - d = 4 - 0 = 4$.
This gives $a=0, b=4, c=4, d=0$.
$A = 2^0 \times 5^4 = 1 \times 625 = 625$. (Units digit 5, not 0).
$B = 2^4 \times 5^0 = 16 \times 1 = 16$. (Units digit 6, not 0).
The product is $625 \times 16 = 10000$. This pair works.
Case 2: $b=0$. From (ii), $d = 4 - b = 4 - 0 = 4$. Now we need (either $c=0$ or $d=0$). Since $d=4 \neq 0$, we must have $c=0$. From (i), $a = 4 - c = 4 - 0 = 4$.
This gives $a=4, b=0, c=0, d=4$.
$A = 2^4 \times 5^0 = 16 \times 1 = 16$. (Units digit 6, not 0).
$B = 2^0 \times 5^4 = 1 \times 625 = 625$. (Units digit 5, not 0).
The product is $16 \times 625 = 10000$. This pair works.
If $a > 0$ and $b > 0$, then $A$ would be divisible by 10. If $c > 0$ and $d > 0$, then $B$ would be divisible by 10. The only combinations satisfying the constraints are the ones found above.
The two numbers are 16 and 625.
Intext Question (Page 127 - 128)
A Prime Puzzle
The figure on the left shows the puzzle. The figure on the right shows the solution of the puzzle. Think what the rules can be to solve the puzzle.

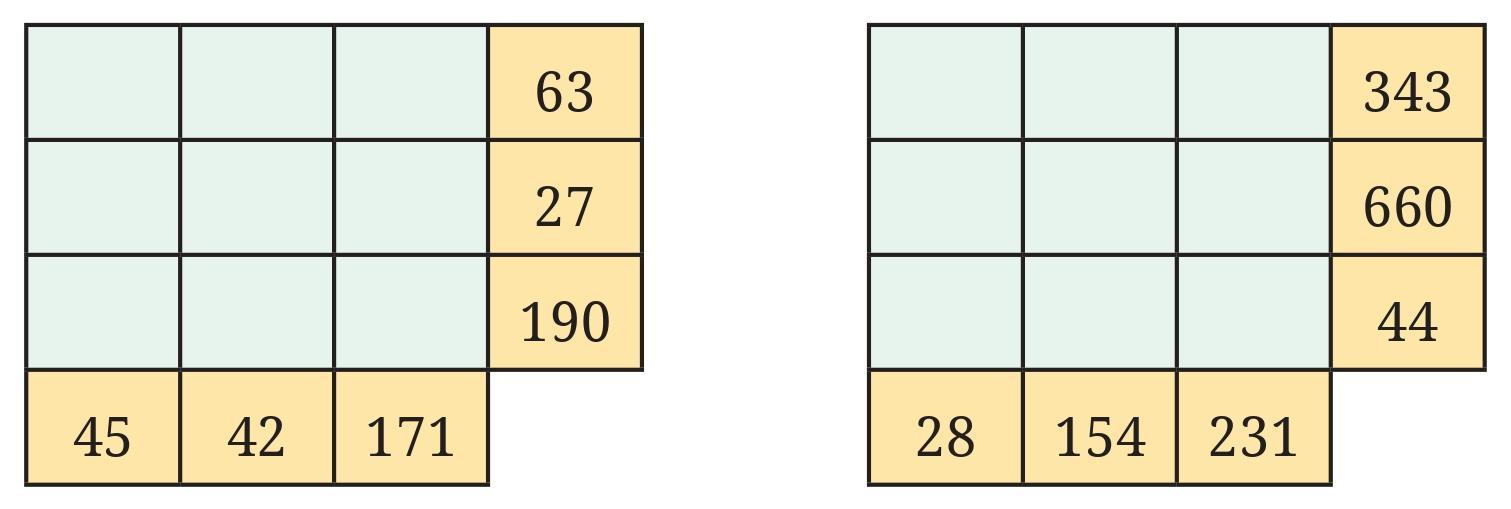
Answer:
The puzzle requires filling a 3x3 grid with numbers, stated as "prime numbers only", such that the product of the numbers in each row and each column matches the given numbers.
The given products are:
Row Products: 30, 77, 143
Column Products: 70, 33, 66
First, let's find the prime factorization of these products:
$30 = 2 \times 3 \times 5$
$77 = 7 \times 11$
$143 = 11 \times 13$
$70 = 2 \times 5 \times 7$
$33 = 3 \times 11$
$66 = 2 \times 3 \times 11$
The grid is 3x3, meaning there are three numbers in each row and column whose product must equal the given number. Since 77, 143, and 33 are products of only two distinct prime numbers, and the numbers in the grid must be prime, one of the numbers in the corresponding row/column must be 1 (as 1 times the two primes gives the required product). While 1 is not strictly a prime number, it is often included in the set of allowed numbers in such puzzles to make them solvable. Let's assume the allowed numbers in the grid are prime numbers greater than 1, or the number 1.
Based on the prime factorizations, the possible numbers that can appear in the grid are from the union of the factors of the products, plus 1 where needed for three factors: $\{1, 2, 3, 5, 7, 11, 13\}$.
Let the grid be denoted by $\begin{pmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & p_{33} \end{pmatrix}$, where $p_{ij} \in \{1, 2, 3, 5, 7, 11, 13\}$.
The set of numbers in each row and column must be permutations of the prime factors (plus 1 where needed):
Row 1: $\{p_{11}, p_{12}, p_{13}\} = \{2, 3, 5\}$
Row 2: $\{p_{21}, p_{22}, p_{23}\} = \{1, 7, 11\}$
Row 3: $\{p_{31}, p_{32}, p_{33}\} = \{1, 11, 13\}$
Column 1: $\{p_{11}, p_{21}, p_{31}\} = \{2, 5, 7\}$
Column 2: $\{p_{12}, p_{22}, p_{32}\} = \{1, 3, 11\}$
Column 3: $\{p_{13}, p_{23}, p_{33}\} = \{2, 3, 11\}$
Let's determine the values of the cells by finding the intersection of the sets for the corresponding row and column:
$p_{12} \in \{2, 3, 5\} \cap \{1, 3, 11\} = \{3\}$. So, $p_{12} = 3$.
$p_{21} \in \{1, 7, 11\} \cap \{2, 5, 7\} = \{7\}$. So, $p_{21} = 7$.
$p_{31} \in \{1, 11, 13\} \cap \{2, 5, 7\} = \{1\}$. So, $p_{31} = 1$.
$p_{33} \in \{1, 11, 13\} \cap \{2, 3, 11\} = \{11\}$. So, $p_{33} = 11$.
Let's place these fixed values in the grid:
$\begin{pmatrix} p_{11} & 3 & p_{13} \\ 7 & p_{22} & p_{23} \\ 1 & p_{32} & 11 \end{pmatrix}$
Now let's use the product constraints for the rows and columns with the determined values:
Row 3 product: $p_{31} \times p_{32} \times p_{33} = 143$
$1 \times p_{32} \times 11 = 143$
$11 p_{32} = 143$
$p_{32} = \frac{143}{11} = 13$
... (i)
So, the value of $p_{32}$ must be 13.
However, let's check the possible values for $p_{32}$ based on its position in the grid, using the intersection of the sets for Row 3 and Column 2:
$p_{32} \in \{1, 11, 13\} \cap \{1, 3, 11\}$
$p_{32} \in \{1, 11\}$
$p_{32} \in \{1, 11\}$
... (ii)
From equation (i), $p_{32}$ must be 13. From equation (ii), $p_{32}$ must be either 1 or 11.
This is a contradiction.
The required value for $p_{32}$ to satisfy the Row 3 product (given the other determined values in that row) is 13, but the possible values for $p_{32}$ based on the intersection of the sets for Row 3 and Column 2 are only 1 or 11.
Conclusion: The puzzle, as stated with the given row and column products (30, 77, 143, 70, 33, 66), cannot be solved by filling the 3x3 grid with prime numbers and 1 such that all product conditions are met. There appears to be an inconsistency in the problem statement itself.
The provided solution image also does not match the given products (e.g., the last row/column products in the image are 715, not 143 and 66).
Therefore, based on the numbers provided in the question text, the puzzle has no solution.

